
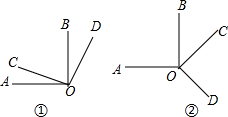
 如图①所示,∠AOB,∠COD都是直角.
如图①所示,∠AOB,∠COD都是直角.

科目:初中数学 来源: 题型:
| 3 |
| 3 |
 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013-2014学年人教版七年级上册数学课后训练:4.3角 题型:044
如图甲所示,∠AOB,∠COD都是直角.
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系,你能用推理的方法说明你的猜想是否合理吗?
(2)当∠COD绕点O旋转到图乙的位置时,你原来的猜想还成立吗?

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com