
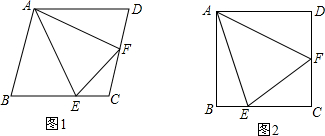
分析 (1)根据菱形的性质得出AC平分∠BCD,再根据角平分线的性质证明即可.
(2)根据正方形的性质和全等三角形的判定和性质证明即可;
(3)根据勾股定理进行解答即可.
解答 解:(1)证明:过点A作AG⊥BC于G,过A作AH⊥EF于H,过A作AM⊥CD于M,连接AC,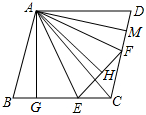
∵四边形ABCD是菱形,
∴AC平分∠BCD,
又∵AG⊥BC,AM⊥CD,
∴AG=AM,
∵∠AEB=∠AEF,
∴AE平分∠BEF,
又∵AG⊥BC,AH⊥EF,
∴AG=AH,
∴AH=AM,
∴AF平分∠EFD;
(2)∵四边形ABCD是菱形,
又∵∠C=90°,
∴四边形ABCD是正方形,
∴∠B=∠D=90°,
∴AB⊥BC,AD⊥CD,
过A作AH⊥EF于H,
∴∠AHE=∠AHF=90°,
∴AE平分∠BEF,
又∵AB⊥BC,AH⊥EF,
∴AB=AH,
∵AE=AE,
在Rt△ABE与Rt△AHE中
$\left\{\begin{array}{l}{AB=AH}\\{AE=AE}\end{array}\right.$,
∴Rt△ABE≌Rt△AHE(HL)
∴BE=HE,
同理Rt△ADF≌Rt△AHF(HL),
∴DF=HF,
∵EF=EH+FH,
∴EF=BE+DF;
(3)设BE=a,则AB=3a,
在Rt△ABE中,BE2+AB2=AE2,
∴${a}^{2}+(3a)^{2}=(2\sqrt{10})^{2}$,
∴a=2,
∴AB=3a=6,
由(2)知四边形ABCD是正方形,
∴BC=CD=AB=6,
∴CE=BC-BE=4,
设DF=m,则CF=CD-DF=6-m,
由(2)知EF=BE+DF,
∴EF=2+m,
在Rt△ECF中,CE2+CF2=EF2,
∴42+(6-m)2=(2+m)2,
∴m=3,
在Rt△ADF中,DF2+AD2=AF2,
∴$AF=\sqrt{{3}^{2}+{6}^{2}}=3\sqrt{5}$.
点评 此题主要考查了菱形的性质,关键是判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 为了了解本校七年级学生的身体素质情况,体育老师随机抽取了本校50名七年级学生进行一分钟跳绳次数测试,测试所得样本数据(单位:次)如下:
为了了解本校七年级学生的身体素质情况,体育老师随机抽取了本校50名七年级学生进行一分钟跳绳次数测试,测试所得样本数据(单位:次)如下:| 组别 | 次数(x) | 频数(人数) |
| 1 | 80≤x<100 | 5 |
| 2 | 100≤x<120 | 10 |
| 3 | 120≤x<140 | 16 |
| 4 | 140≤x<160 | 13 |
| 5 | 160≤x<180 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com