

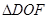 和
和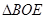 中,
中,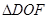 ≌
≌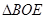 ,所以OE=OF,又因为EF⊥BD,OD=OB,
,所以OE=OF,又因为EF⊥BD,OD=OB,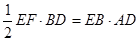 ,
,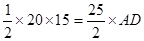 ,所以得AD=12,
,所以得AD=12,

 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
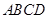 中,
中,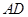 ∥
∥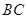 ,
,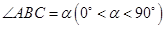 ,
,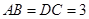 ,
,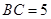 .点
.点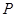 为射线
为射线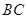 上动点(不与点
上动点(不与点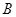 、
、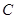 重合),点
重合),点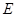 在直线
在直线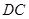 上,且
上,且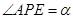 .记
.记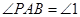 ,
,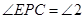 ,
,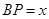 ,
,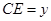 .
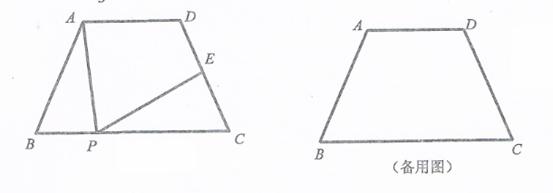
.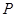 在线段
在线段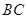 上时,写出并证明
上时,写出并证明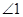 与
与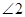 的数量关系;
的数量关系;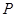 的运动,(1)中得到的关于
的运动,(1)中得到的关于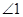 与
与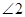 的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的
的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的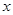 的取值范围;
的取值范围;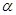 =
=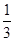 ,试用
,试用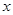 的代数式表示
的代数式表示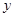 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
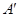 处,折痕为PQ,当点
处,折痕为PQ,当点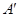 在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点
在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点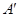 在BC边上可移动的最大距离为 .
在BC边上可移动的最大距离为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com