
【题目】如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当 ![]() 时,求
时,求 ![]() 的值;
的值;
(2)如图②当DE平分∠CDB时,求证:AF= ![]() OA;
OA;
(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG= ![]() BG.
BG.
【答案】
(1)
解:∵ ![]() ,
,
∴ ![]() .
.
∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,
∴△CEF∽△ADF,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ;
;
(2)
证明:∵DE平分∠CDB,∴∠ODF=∠CDF,
又∵AC、BD是正方形ABCD的对角线.
∴∠ADO=∠FCD=45°,∠AOD=90°,OA=OD,而∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,
∴∠ADF=∠AFD,∴AD=AF,
在直角△AOD中,根据勾股定理得:AD= ![]() =
= ![]() OA,
OA,
∴AF= ![]() OA
OA
(3)
证明:连接OE.
∵点O是正方形ABCD的对角线AC、BD的交点.
∴点O是BD的中点.
又∵点E是BC的中点,
∴OE是△BCD的中位线,
∴OE∥CD,OE= ![]() CD,
CD,
∴△OFE∽△CFD.
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
又∵FG⊥BC,CD⊥BC,
∴FG∥CD,
∴△EGF∽△ECD,
∴ ![]() =
= ![]() =
= ![]() .
.
在直角△FGC中,∵∠GCF=45°.
∴CG=GF,
又∵CD=BC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
∴CG= ![]() BG.
BG.

【解析】(1)利用相似三角形的性质求得EF与DF的比值,依据△CEF和△CDF同高,则面积的比就是EF与DF的比值,据此即可求解;(2)利用三角形的外角和定理证得∠ADF=∠AFD,可以证得AD=AF,在直角△AOD中,利用勾股定理可以证得;(3)连接OE,易证OE是△BCD的中位线,然后根据△FGC是等腰直角三角形,易证△EGF∽△ECD,利用相似三角形的对应边的比相等即可证得.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A.x2﹣2是二次二项式
B.单项式﹣x2的系数是1
C.使式子 ![]() 有意义的x的取值范围是x>﹣2
有意义的x的取值范围是x>﹣2
D.若分式 ![]() 的值等于0,则a=±1
的值等于0,则a=±1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号)
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为 . 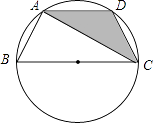
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线 ![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC. 
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC= ![]() ,tan∠AEC=
,tan∠AEC= ![]() ,求圆的直径.
,求圆的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com