
分析 多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.依此即可求解.
解答 解:(1)(x-6)(x-3)
=x2-3x-6x+18
=x2-9x+18;
(2)(x+$\frac{1}{2}$)(x-$\frac{1}{3}$)
=x2-$\frac{1}{3}$x+$\frac{1}{2}$x-$\frac{1}{6}$
=x2+$\frac{1}{6}$x-$\frac{1}{6}$;
(3)(2x+1)(x-3)
=2x2-6x+x-3
=2x2-5x-3;
(4)(x-2)(x2+4)=x3+4x-2x2-8.
点评 此题考查了多项式与多项式相乘,运用法则时应注意以下两点:①相乘时,按一定的顺序进行,必须做到不重不漏;②多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
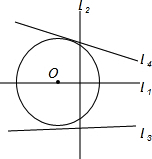 如图,平面上⊙O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是( )
如图,平面上⊙O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是( )| A. | Ll | B. | L2 | C. | L3 | D. | L4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
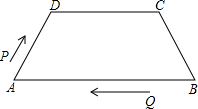 如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为( )
如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为( )| A. | 4s | B. | 3 s | C. | 2 s | D. | 1s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com