
分析 如图,⊙O经过点C且与边AB相切,作OD⊥AB于D,根据切线的性质得OD为⊙O的半径,讨论:当E、F点都不与点C重合,证明EF为⊙O的直径,利用OC+OD≥CD(当点C、O、D共线时,取等号)得到当CD⊥AB时,EF最小,然后计算出此时CD的长得到EF的最小值为$\frac{12}{5}$;当F点与C点重合时,利用相似比求此时圆的半径,得到EF的最大值$\frac{24}{7}$,于是得到线段EF的取值范围.
解答 解: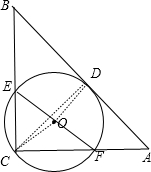 如图,⊙O经过点C且与边AB相切,作OD⊥AB于D,则OD为⊙O的半径,
如图,⊙O经过点C且与边AB相切,作OD⊥AB于D,则OD为⊙O的半径,
当E、F点都不与点C重合,
∵∠ECF=90°,
∴EF为⊙O的直径,
∴OC+OD=EF,
而OC+OD≥CD(当点C、O、D共线时,取等号),
∴当CD⊥AB时,EF最小,
此时CD=$\frac{AC•BC}{AB}$=$\frac{12}{5}$,
∴EF的最小值为$\frac{12}{5}$,
当F点与C点重合时,EF最大,此时设圆的半径为r,则r:3=(4-r):5,解得r=$\frac{12}{7}$,所有EF的最大值为$\frac{24}{7}$,
∴线段EF的取值范围为$\frac{12}{5}$≤EF≤$\frac{24}{7}$.
故答案为$\frac{12}{5}$≤EF≤$\frac{24}{7}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
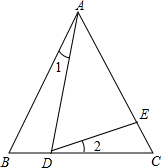 如图,已知等边三角形ABC的边长为4,D在BC边上,BD=$\frac{1}{3}$CD,∠1=∠2.
如图,已知等边三角形ABC的边长为4,D在BC边上,BD=$\frac{1}{3}$CD,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
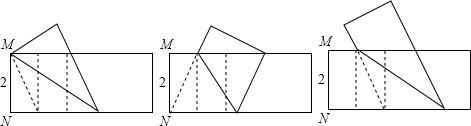
| A. | 0种 | B. | 1种 | C. | 2种 | D. | 3种 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
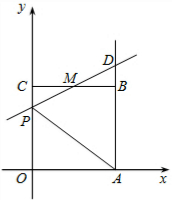 矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根
矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 队伍/场次 | 1 | 2 | 3 | 4 | 5 |
| 北方队 | 和2:2 | 胜3:1 | 负0:1 | 胜2:1 | 胜3:2 |
| 风暴队 | 胜3:2 | 负0:2 | 胜2:1 | 和2:2 | 和2:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P为长方形ABCD内一点,连接PA、PB、PC、PD和BD,其中BD、PC交于点Q.若△DPQ和△ABP的面积分别为4.2和20.2,则△BCQ的面积为24.4.
如图,点P为长方形ABCD内一点,连接PA、PB、PC、PD和BD,其中BD、PC交于点Q.若△DPQ和△ABP的面积分别为4.2和20.2,则△BCQ的面积为24.4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com