
 如图,有一斜坡AB长170m,坡顶离地面的高度BC为80m,求此斜坡的水平距离AC的长度.
如图,有一斜坡AB长170m,坡顶离地面的高度BC为80m,求此斜坡的水平距离AC的长度.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
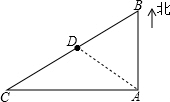 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏.
如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑.因施工需要,必须在A处进行一次爆破.为使民房、变电设施、古建筑都不遭到破坏.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
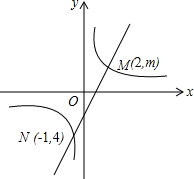 如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于M(2,m)、N(-1,-4)两点.求:
如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于M(2,m)、N(-1,-4)两点.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
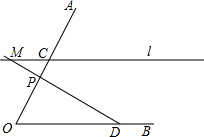 如图,已知C、D分别是∠AOB的边OA和OB上两个定点,过点C的直线ι∥OB,P是边OA上的一个动点,射线DP交直线l于点M,tan∠AOB=2,l与OB的距离等于6,OD=10.
如图,已知C、D分别是∠AOB的边OA和OB上两个定点,过点C的直线ι∥OB,P是边OA上的一个动点,射线DP交直线l于点M,tan∠AOB=2,l与OB的距离等于6,OD=10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
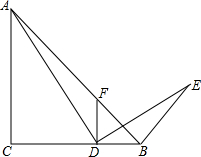 如图,在△ABC中,∠C=90°,AC=BC,点D在BC边上,连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE,作DF⊥BC交AB于点F.
如图,在△ABC中,∠C=90°,AC=BC,点D在BC边上,连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE,作DF⊥BC交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
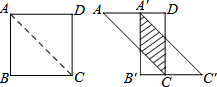 如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )
如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )| A. | 6cm | B. | 8cm | C. | 6cm或8cm | D. | 4cm或8cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com