
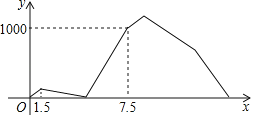
【题目】甲乙两人从A地出发去相距1800米的B地,甲出发1.5分钟后乙再出发,在中途乙追上甲,追上甲后,乙发现有东西忘带了,于是以原来1.2倍的速度返回,甲则继续以原速度前行,乙返回A地后取东西花了2分钟,取完东西后立即以返回时的速度追甲,甲达到B地以后立即返回,并与乙在途中相遇,设甲乙两人之间的距离为y(米),甲出发的时间为x(分钟),y与x的关系如图所示,则当甲乙两人第二次相遇时,两人距B地的距离为_____米.
【答案】![]()
【解析】
由题意,甲的速度为1000÷7.5=![]() 米/分,再根据路程的关系求得乙返回时的速度为
米/分,再根据路程的关系求得乙返回时的速度为![]() 米/分,根据相遇问题中的数量关系得到甲、乙两人最后相遇时,乙距B地的路程.
米/分,根据相遇问题中的数量关系得到甲、乙两人最后相遇时,乙距B地的路程.
解:设乙原来的速度为a米/分,b分时,乙第一次追上甲,
由图可知:7.5分时,乙取东西返回时到A地,此时,甲、乙相距1000米,即甲7.5分走了1000米,
∴甲的速度是:![]() (米/分),
(米/分),
根据题意得: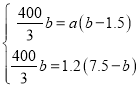 ,
,
解得:a(b﹣1.5)=1.2a(7.5﹣b),
b=![]() ,1.2a=
,1.2a=![]() ,
,
即乙返回时的速度为![]() 米/分,
米/分,
设甲和乙第二次相遇的时间为m分,
(m﹣7.5﹣2)×![]() +(m﹣7.5)×
+(m﹣7.5)×![]() =1800+1800﹣1000,
=1800+1800﹣1000,
m=![]() ,
,
1800﹣(![]() ﹣7.5﹣2)×
﹣7.5﹣2)×![]() =
=![]() .
.
则当甲乙两人第二次相遇时,两人距B地的距离为![]() 米.
米.
故答案为:![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
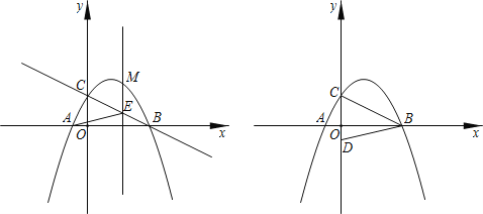
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0)、B(4,0)与y轴交于点C,tan∠ABC=![]() .
.
(1)求抛物线的解析式;
(2)点M在第一象限的抛物线上,ME平行y轴交直线BC于点E,连接AC、CE,当ME取值最大值时,求△ACE的面积.
(3)在y轴负半轴上取点D(0,-1),连接BD,在抛物线上是否存在点N,使∠BAN=∠ACO-∠OBD?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
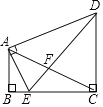
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,AB=1,AE⊥AD,交BC于点E,EA平分∠BED.
(1)CD的长是_____;
(2)当点F是AC中点时,四边形ABCD的周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
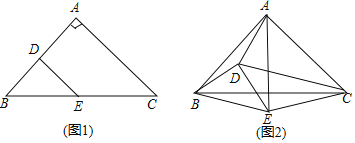
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=2,点D、E分别是AB、BC的中点,把△BDE绕点B旋转,连接AD、AE、CD、CE,如图2.
(1)求证:△BDE∽△BAC.
(2)求△ABE面积最大时,△ADE的面积.
(3)在旋转过程中,当点D落在△ACE的边所在直线上时,直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题:
材料一:平面直角坐标系中,对点A(x1,y1),B(x2,y2)定义一种新的运算:AB=x1x2+y1y2,例如:若A(1,2),B(3,4),则AB=1×3+2×4=11
材料二:平面直角坐标系中,过横坐标不同的两点A(x1,y1),B(x2,y2)的直线的斜率为kAB=![]() ,由此可以发现:若kAB=
,由此可以发现:若kAB=![]() =1,则有y1﹣y2=x1﹣x2,即x1﹣y1=x2﹣y2,反之,若x1,x2,y1,y2,满足关系式x1﹣y1=x2﹣y2,则有y1﹣y2=x1﹣x2,那么kAB=
=1,则有y1﹣y2=x1﹣x2,即x1﹣y1=x2﹣y2,反之,若x1,x2,y1,y2,满足关系式x1﹣y1=x2﹣y2,则有y1﹣y2=x1﹣x2,那么kAB=![]() =1.
=1.
(1)已知点M(﹣2,﹣6),N(3,﹣2),则MN= ,若点A,B的坐标分别为(x1,y1),(x2,y2)(x1≠x2),且满足关系式2x1+y1=2x2+y2,那么kAB= ;
(2)如图,横坐标互不相同的三个点C,D,E满足CD=DE,且D点是直线y=x上第一象限内的点,点D到原点的距离为2![]() .过点D作DF∥y轴,交直线CE于点F,若DF=6,请结合图象,求直线CE、直线DF与两坐标轴围成的四边形面积.
.过点D作DF∥y轴,交直线CE于点F,若DF=6,请结合图象,求直线CE、直线DF与两坐标轴围成的四边形面积.
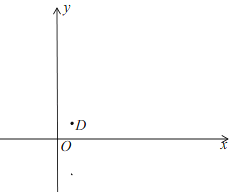
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,![]() 的最小值为0;
的最小值为0;![]() .当
.当![]() 时有
时有![]() ;且对于任意实数
;且对于任意实数![]() ,
,![]() .
.
(1)![]() 的对称轴为_________,顶点坐标为_____________;
的对称轴为_________,顶点坐标为_____________;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)令![]() ,试求实数
,试求实数![]() ,使得实数
,使得实数![]() 最大,当
最大,当![]() 时
时![]() 成立.
成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
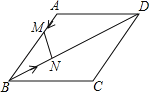
【题目】如图所示,菱形ABCD的边长是2厘米,∠BAD=120°,动点M以1厘米/秒的速度自A点出发向B移动,动点N以2厘米/移的速度自B点出发向D移动,两点中任一个到达线段端点移动便告结束.若点M、N同时出发运动了t秒,记△BMN的面积为S厘米2,下面图象中能表示S与t之间的函数关系的是( )
A.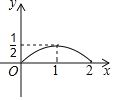 B.
B.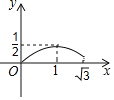
C.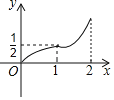 D.
D.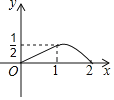
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四 边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在X轴上,直线BD交Y轴于点F,交OE于点H,线段BC、OC的长是方程x2-6x+8=0的两个根,且OC>BC.
(1)求直线BD的解析式.
(2)求 △OFH的面积.
(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com