
【题目】已知:在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 和
和![]() .
.
(1)若点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上且与点
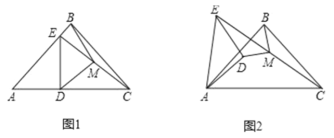
上且与点![]() 不重合,如图1,探索
不重合,如图1,探索![]() 的关系并给予证明;
的关系并给予证明;
(2)如果将图1中的![]() 绕点
绕点![]() 逆时针旋转小于
逆时针旋转小于![]() 的角,如图2,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.
的角,如图2,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.
【答案】(1)![]() ,
,![]() ,见解析;(2)(1)中的结论仍成立,见解析
,见解析;(2)(1)中的结论仍成立,见解析
【解析】
(1)要求BM和DM的关系,可从角的度数入手,由题意,BM是直角三角形CBE斜边上的中线,因此BM=CM,∠MCB=∠MBC,∠BME=2∠MCB,同理可得出∠DME=2∠DCM,根据三角形ABC是个等腰直角三角形,那么∠DCM+∠BCE=45°,因此∠BME+∠DME=2(∠DCM+∠BCM)=90°,由此我们可得出∠BMD=90°,那么BM和DM是互相垂直的;
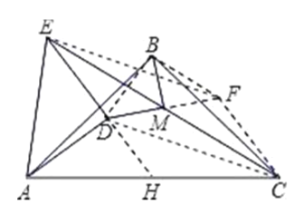
(2)可通过构建三角形来求解,连接CD和EF,连接BD,延长DM至点F,使得DM=MF,连接BF、FC,延长ED交AC于点H,先证明三角形ADB和CFB全等后,再证明三角形DBF是等腰三角形,即可得出BM⊥DM.
解:(1)![]() ,
,![]() ,
,
在![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,
的中点,
∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() .
.
(2):(1)中的结论仍成立,
延长![]() 至点
至点![]() ,使得
,使得![]() ,连接
,连接![]() 和
和![]() ,连接
,连接![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∵![]()
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
在![]() 中,由
中,由![]() ,
,![]() ,得
,得![]() 且
且![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】学校打算用长![]() 米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为
米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为![]() 米的墙上(如图).
米的墙上(如图).

(1)若生物园的面积为![]() 平方米,求生物园的长和宽;
平方米,求生物园的长和宽;
(2)能否围城面积为![]() 平方米的生物园?若能,求出长和宽;若不能,请说明理由.
平方米的生物园?若能,求出长和宽;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中△ABC三个顶点的坐标分别是点A(﹣2,3)、点B(﹣1,1)、点C(0,2).
(1)作△ABC关于C成中心对称的△A1B1C1;
(2)将△A1B1C1向右平移3个单位,作出平移后的△A2B2C2;
(3)在x轴上求作一点P,使PA1+PC1的值最小,并写出点 P 的坐标.(不写解答过程,直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
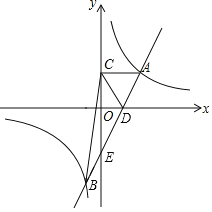
【题目】如图,直线y=ax﹣a与双曲线y=![]() (k>0)交于A、B两点,与x轴交于点D,与y轴交于点E,AC⊥y轴,垂足为点C.已知S△ACD=2,B(﹣1,m)
(k>0)交于A、B两点,与x轴交于点D,与y轴交于点E,AC⊥y轴,垂足为点C.已知S△ACD=2,B(﹣1,m)
(1)直接写出a与k的值.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
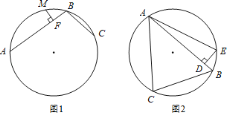
【题目】定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.
如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
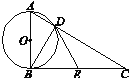
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,E是BC的中点,连接BD,DE.
(1)若![]() ,求sinC;
,求sinC;
(2)求证:DE是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com