
分析 (1)先计算二次根式的乘法和除法,再合并可得;
(2)先计算完全平方和平方差,再去括号、合并可得.
解答 解:(1)原式=3$\sqrt{2}$+$\sqrt{2}$+$\frac{\sqrt{2}}{2}$=$\frac{9\sqrt{2}}{2}$;
(2)原式=9+6$\sqrt{5}$+5-(5-1)
=9+6$\sqrt{5}$+5-5+1
=10+6$\sqrt{5}$.
点评 本题主要考查二次根式的混合运算,二次根式的混合运算应注意以下几点:
①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式“,多个不同类的二次根式的和可以看作“多项式“.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:选择题
| A. | x+1=(26-x)-2 | B. | x+1=(13-x)-2 | C. | x-1=(26-x)+2 | D. | x-1=(13-x)+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
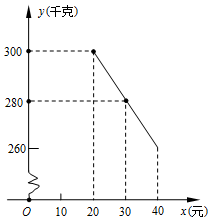 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com