
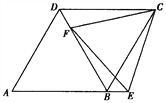
【题目】如图,在菱形ABCD中,点F为对角线BD上一点,点E为AB的延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.
【答案】(1)证明见解析;(2)∠CFE=60°.
【解析】(1)根据菱形的性质得出CD=CB,又DF=BE,CF=CE,根据SSS即可证明△CFD≌△CEB;
(2)根据全等三角形、菱形的性质得出∠ABD=∠CBD=∠CDB=∠CBE,由平角的定义求出∠ABD=∠CBD=60°,再证明∠FCE=60°,那么由CF=CE,得出△AFE是等边三角形,于是∠CFE=60°.
证明:(1)∵四边形 ABCD是菱形,∴CD=CB.
在△CFD和△CEB中, 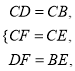 ∴△CFD≌△CEB.
∴△CFD≌△CEB.
(2)∵△CFD≌△CEB,∴∠CDB=CBE, ∠DCF=∠BCE.∵CD=CB,
∴∠CDB=∠CBD,∴∠ABD=∠CBD=∠CBE=60°,∴∠DCB=60°,
∴∠FCE=∠FCB+∠BCE=∠FCB+∠DCF=60°.
又CF=CE,∴△CFE为等边三角形,∴∠CFE=60°.
“点睛”本题考查了菱形的性质:①菱形具有平行四边形的一般性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了全等三角形、等边三角形的判定与性质.


科目:初中数学 来源: 题型:
【题目】如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A、C、B′三点共线,那么旋转角度的大小为( )
A.45°
B.90°
C.120°
D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1 , 再将点P1绕原点旋转90°得到点P2 , 则点P2的坐标是( )
A.(3,﹣3)
B.(﹣3,3)
C.(3,3)或(﹣3,﹣3)
D.(3,﹣3)或(﹣3,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=x+6,下列结论错误的是( )
A.函数值随自变量增大而增大
B.函数图象与x轴正方向成45°角
C.函数图象不经过第四象限
D.函数图象与x轴交点坐标是(0,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
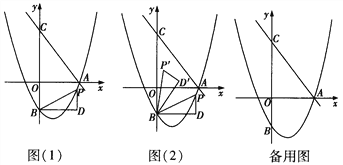
【题目】如图(1),直线![]() 交x轴于点A,交
交x轴于点A,交![]() 轴于点C(0,4),抛物线
轴于点C(0,4),抛物线![]() 过点A,交y轴于点B(0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为
过点A,交y轴于点B(0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图(2),将△BDP绕点B 逆时针旋转,得到△BD′P′,当旋转角∠PBP′=∠OAC,且点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com