
【题目】某校为了了解八年级学生对![]() (科学)、
(科学)、![]() (技术)、
(技术)、![]() (工程)、
(工程)、![]() (艺术)、
(艺术)、![]() (数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
(数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
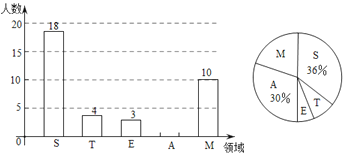
(1)这次抽样调查共调查了多少名学生?
(2)补全条形统计图;
(3)求扇形统计图中![]() (数学)所对应的圆心角度数;
(数学)所对应的圆心角度数;
(4)若该校八年级学生共有400人,请根据样本数据估计该校八年级学生中对![]() (科学)最感兴趣的学生大约有多少人?
(科学)最感兴趣的学生大约有多少人?
【答案】(1)50;(2)见解析;(2)![]() ;(3)144人.
;(3)144人.
【解析】
(1)根据S(科学),的人数除以百分比,计算即可;
(2)求出A组人数,画出条形图即可;
(3)根据圆心角=360°×百分比计算即可;
(4)利用样本估计总体的思想解决问题即可;
(1)18÷36%=50(人),
答:这次抽样调查共调查了50名学生.
(2)A组人数=50-18-4-3-10=15,
条形图如图所示:
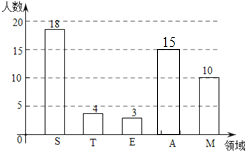
(3)10÷50×100%=20%,
360°×20%=72°,
答:扇形统计图中M(数学)所对应的圆心角度数为72°.
(4)400×36%=144(人),
答:根据样本数据估计该校八年级学生中对S(科学)最感兴趣的学生大约有144人.


科目:初中数学 来源: 题型:
【题目】市教育局决定分别配发给一中8台电脑,二中10台电脑,但现在仅有12台,需
在商场购买6台. 从市教育局运一台电脑到一中、二中的运费分别是30元和50元,从商场
运一台电脑到一中、二中的运费分别是40元和80元. 要求总运费不超过840元,问有几
种调运方案?指出运费最低的方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)求证:△BCE≌△DCF;
(2)求CF的长。
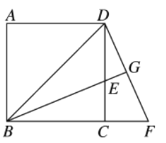
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
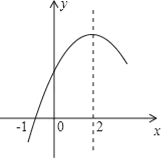
其中正确结论的序号是_______________.(在横线上填上你认为所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)9x2-100=0 (2)x(x-1)=2(x-1)
(3)(x+2)(x+3)=20 (4)3x2-4x-1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
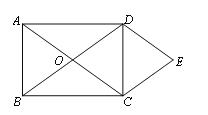
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新合作超市最近进了一批玩具,进价每个15元,今天共卖山20个,实际卖出的价格以每个18元为标准,超过的记为正,不足的记为负,记录如下:
实际每个售出价格与标准的差值(单位:元) | +3 | -1 | +2 | +1 |
个数 | 5 | 4 | 6 | 5 |
(1)这个超市今天卖出玩具的平均价格是多少?
(2)这个超市今天卖出的玩具赚了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com