
如图,直线 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于A、B两点,正比例函数
轴正半轴分别交于A、B两点,正比例函数 的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
(1)求A、B两点的坐标;(用b表示)
(2)图中有全等的三角形吗?若有,请找出并说明理由。
(3)求MN的长.

解: (1)直线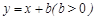 与
与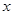 轴的交点坐标A为(-b,0),
轴的交点坐标A为(-b,0),
与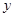 轴的交点坐标B为(0,b)
轴的交点坐标B为(0,b)
(2)有,△MAO≌△NOB。理由:
由(1)知OA=OB
∵AM⊥OQ,BN⊥OQ ∴∠AMO=∠BNO=90°
∵∠MOA+∠MAO=90°,∠MOA+∠MOB=90°
∴∠MAO=∠MOB
在△MAO和△BON中
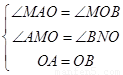
∴△MAO≌△NOB
(3)∵△MAO≌△NOB
∴OM=BN,AM=ON
∴MN=ON-OM=AM-BN=7
【解析】(1)分别令y=0,x=0来求直线y=x+b(b>0)与x轴负半轴、y轴正半轴的交点A、B的坐标;
(2)利用全等三角形的判定定理ASA判定△MAO≌△NOB;
(3)根据全等三角形△MAO≌△NOB的对应边相等推知OM=BN,AM=ON,从而求得MN=ON-OM=AM-BN=7.


科目:初中数学 来源: 题型:
 ,点N是x轴负半轴上的一点,NH⊥CM,交CM(或CM的延长线)于点H,交y轴于点D,且ND=CM.
,点N是x轴负半轴上的一点,NH⊥CM,交CM(或CM的延长线)于点H,交y轴于点D,且ND=CM.查看答案和解析>>
科目:初中数学 来源: 题型:
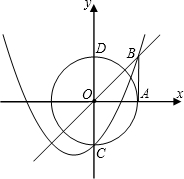 圆与y轴相交于点C、D,抛物线y=x2+px+q经过点B、C.
圆与y轴相交于点C、D,抛物线y=x2+px+q经过点B、C.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |

查看答案和解析>>
科目:初中数学 来源:2011-2012学年吉林省东丰县八年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,直线 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于A、B两点,正比例函数
轴正半轴分别交于A、B两点,正比例函数 的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
(1)求A、B两点的坐标;(用b表示)
(2)图中有全等的三角形吗?若有,请找出并说明理由。
(3)求MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com