
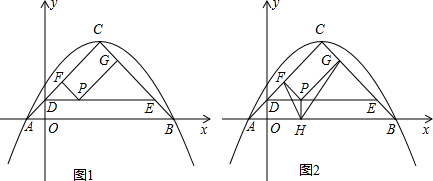
ЗжЮі ЃЈ1ЃЉНЋBЃЈ7ЃЌ0ЃЉДњШыy=mx2+ЃЈ2m+2ЃЉx+m+2ЃЌЕУЕН49m+7ЃЈ2m+2ЃЉ+m+2=0ЃЌНтЗНГЬЧѓГіmЕФжЕЃЌЧѓЕУХзЮяЯпЕФНтЮіЪНЃЌдйРћгУХфЗНЗЈНЋвЛАуЪНЛЏЮЊЖЅЕуЪНЃЌМДПЩЧѓГіЖЅЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЯШЧѓГіAЕузјБъЃЌРћгУСНЕуМфЕФОрРыЙЋЪНЕУЕНAC2=32ЃЌBC2=32ЃЌAB2=82=64ЃЌФЧУДЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЕУЕНЁЯCAB=ЁЯCBA=45ЁуЃЌЁЯC=90ЁуЃЌOD=OA=1ЃЌAD=$\sqrt{2}$ЃЌCD=AC-AD=3$\sqrt{2}$ЃЌDE=$\sqrt{2}$CD=6ЃЎдйжЄУїЁїPDFЃЌЁїPEGЃЌЁїDECЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЫФБпаЮCFPGЪЧОиаЮЃЎгЩDP=aЃЌPE=DE-DP=6-aЃЌЧѓГіPF=$\frac{\sqrt{2}}{2}$DP=$\frac{\sqrt{2}}{2}$aЃЌPG=$\frac{\sqrt{2}}{2}$PE=$\frac{\sqrt{2}}{2}$ЃЈ6-aЃЉЃЌШЛКѓИљОнОиаЮCFPGЕФУцЛ§=PF•PGЃЌМДПЩЕУЕНyгыaЕФКЏЪ§ЙиЯЕЪНЃЌдйИљОнЖўДЮКЏЪ§ЕФаджЪЧѓГіyЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЯШгЩЁЯFPH=ЁЯGPH=90Ёу+45Ёу=135ЁуЃЌПЩжЊЕБЁїPFHгыЁїPHGЯрЫЦЪБЃЌЗжСНжжЧщПіНјааЬжТлЃКЂйЁїPFHЁзЁїPHGЃЛЂкЁїPFHЁзЁїPGHЃЎИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§СаГіБШР§ЪНЧѓГіaЕФжЕЃЌНјЖјЕУЕНPЕузјБъЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпХзЮяЯпy=mx2+ЃЈ2m+2ЃЉx+m+2гыxжсНЛгкЕуBЃЈ7ЃЌ0ЃЉЃЌ
Ёр49m+7ЃЈ2m+2ЃЉ+m+2=0ЃЌ
НтЕУm=-$\frac{1}{4}$ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+$\frac{7}{4}$ЃЌ
Ёпy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+$\frac{7}{4}$=-$\frac{1}{4}$ЃЈx2-6x+9ЃЉ+$\frac{9}{4}$+$\frac{7}{4}$=-$\frac{1}{4}$ЃЈx-3ЃЉ2+4ЃЌ
ЁрЖЅЕуCЕФзјБъЮЊЃЈ3ЃЌ4ЃЉЃЛ
ЃЈ2ЃЉЁпy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+$\frac{7}{4}$ЃЌ
ЁрЕБy=0ЪБЃЌ-$\frac{1}{4}$x2+$\frac{3}{2}$x+$\frac{7}{4}$=0ЃЌ
НтЕУx1=-1ЃЌx2=7ЃЌ
ЁпBЃЈ7ЃЌ0ЃЉЃЌ
ЁрAЃЈ-1ЃЌ0ЃЉЃЎ
ЁпAC2=ЃЈ3+1ЃЉ2+42=32ЃЌBC2=ЃЈ3-7ЃЉ2+42=32ЃЌAB2=82=64ЃЌ
ЁрAC=BC=4$\sqrt{2}$ЃЌAC2+BC2=AB2ЃЌ
ЁрЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯCAB=ЁЯCBA=45ЁуЃЌЁЯC=90ЁуЃЌ
ЁрOD=OA=1ЃЌAD=$\sqrt{2}$ЃЌCD=AC-AD=3$\sqrt{2}$ЃЌDE=$\sqrt{2}$CD=6ЃЎ
ЁпDEЁЮABЃЌPFЁЭACгкFЃЌPGЁЭBCгкGЃЌ
ЁрЁїPDFЃЌЁїPEGЃЌЁїDECЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЫФБпаЮCFPGЪЧОиаЮЃЎ
ЁпDP=aЃЌPE=DE-DP=6-aЃЌ
ЁрPF=$\frac{\sqrt{2}}{2}$DP=$\frac{\sqrt{2}}{2}$aЃЌPG=$\frac{\sqrt{2}}{2}$PE=$\frac{\sqrt{2}}{2}$ЃЈ6-aЃЉЃЎ
ЁпОиаЮCFPGЕФУцЛ§=PF•PGЃЌ
Ёрy=$\frac{\sqrt{2}}{2}$a•$\frac{\sqrt{2}}{2}$ЃЈ6-aЃЉ=-$\frac{1}{2}$a2+3aЃЌ МДyгыaЕФКЏЪ§ЙиЯЕЪНЮЊy=-$\frac{1}{2}$a2+3aЃЌ
МДyгыaЕФКЏЪ§ЙиЯЕЪНЮЊy=-$\frac{1}{2}$a2+3aЃЌ
ЕБx=$\frac{-3}{2ЁСЃЈ-\frac{1}{2}ЃЉ}$=3ЪБЃЌyгазюДѓжЕ=$\frac{4ЁСЃЈ-\frac{1}{2}ЃЉЁС0-{3}^{2}}{4ЁСЃЈ-\frac{1}{2}ЃЉ}$=$\frac{9}{2}$ЃЛ
ЃЈ3ЃЉЁпЁЯFPH=ЁЯGPH=90Ёу+45Ёу=135ЁуЃЌ
ЁрЕБЁїPFHгыЁїPHGЯрЫЦЪБЃЌПЩЗжСНжжЧщПіНјааЬжТлЃК
ЂйШчЙћЁїPFHЁзЁїPHGЃЌФЧУД$\frac{PF}{PH}$=$\frac{PH}{PG}$ЃЌМД$\frac{\frac{\sqrt{2}}{2}a}{1}$=$\frac{1}{\frac{\sqrt{2}}{2}ЃЈ6-aЃЉ}$ЃЌ
НтЕУa=3ЁР$\sqrt{7}$ЃЌ
ЫљвдPЕузјБъЮЊP1ЃЈ3+$\sqrt{7}$ЃЌ1ЃЉЃЌP2ЃЈ3-$\sqrt{7}$ЃЌ1ЃЉЃЛ
ЂкШчЙћЁїPFHЁзЁїPGHЃЌФЧУД$\frac{PF}{PG}$=$\frac{PH}{PH}$ЃЌМД$\frac{\frac{\sqrt{2}}{2}a}{\frac{\sqrt{2}}{2}ЃЈ6-aЃЉ}$=1ЃЌ
НтЕУa=3ЃЌ
ЫљвдPЕузјБъЮЊP3ЃЈ3ЃЌ1ЃЉЃЎ
злЩЯЫљЪіЃЌЫљЧѓPЕузјБъЮЊP1ЃЈ3+$\sqrt{7}$ЃЌ1ЃЉЃЌP2ЃЈ3-$\sqrt{7}$ЃЌ1ЃЉЃЌP3ЃЈ3ЃЌ1ЃЉЃЎ
ЕуЦР БОЬтЪЧЖўДЮКЏЪ§ЕФзлКЯЬтаЭЃЌЦфжаЩцМАЕНРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЌХзЮяЯпЕФаджЪЃЌСНЕуМфЕФОрРыЙЋЪНЃЌЦНааЯпЕФаджЪЃЌЕШбќжБНЧШ§НЧаЮЁЂОиаЮЁЂЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЕШжЊЪЖЃЌдкЧѓгаЙиЖЏЕуЮЪЬтЪБвЊзЂвтЗжЮіЬтвтЗжЧщПіЬжТлНсЙћЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 10 | BЃЎ | 20 | CЃЎ | 30 | DЃЎ | 40 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
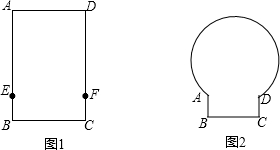
 ШчЭМЃЌЁбOЕФжБОЖAB=6ЃЌЕуCЮЊЁб0ЭтвЛЕуЃЌCAЁЂCBЗжБ№НЛЁбOгкEЁЂFЃЌcosЁЯC=$\frac{2}{3}$ЃЌдђEFЕФГЄЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌЁбOЕФжБОЖAB=6ЃЌЕуCЮЊЁб0ЭтвЛЕуЃЌCAЁЂCBЗжБ№НЛЁбOгкEЁЂFЃЌcosЁЯC=$\frac{2}{3}$ЃЌдђEFЕФГЄЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 3 | BЃЎ | 2 | CЃЎ | 1.5 | DЃЎ | 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌЖўДЮКЏЪ§y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$ЕФЭМЯѓНЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЌЖЅЕуЮЊDЃЎ
ШчЭМЃЌЖўДЮКЏЪ§y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$ЕФЭМЯѓНЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЌЖЅЕуЮЊDЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com