
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | a≥-1 | B. | a≤1 | C. | 0<a≤1 | D. | -1≤a≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数段(x分) | x≤10 | 11≤x≤15 | 16≤x≤20 | 21≤x≤25 | 26≤x≤30 |
| 人 数 | 10 | 15 | 35 | 112 | 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
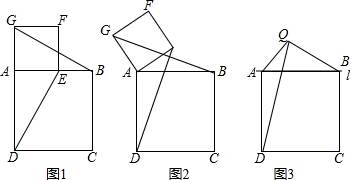
 如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.
如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
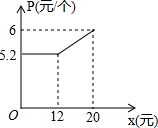 某企业接到一批零件的加工任务,要求在20天内完成,这批零件的出厂价为每个6元.为按时完成任务,该企业招收了新工人,在6天的培训期内,新工人小亮第x天能加工80x个零件,培训后小亮第x天内加工的零件个数为(50x+200)个.
某企业接到一批零件的加工任务,要求在20天内完成,这批零件的出厂价为每个6元.为按时完成任务,该企业招收了新工人,在6天的培训期内,新工人小亮第x天能加工80x个零件,培训后小亮第x天内加工的零件个数为(50x+200)个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com