
分析 首先分析梯形的底和腰的长度分别是什么.如图,平移AB至DE,根据三角形三边关系讨论△CDE三边的取值可能性,确定梯形的底和腰的长度.经探究只有底为1和4,腰为3和4成立.再在△CDE中运用等积法求梯形的高后求面积.
解答 解:根据题意,梯形的两底长分别为2cm和5cm,腰分别为3cm和4cm,如图所示,AD=,BC=4,AB=2,CD=3.作DE∥AB于点E,CF⊥ED于F,DH⊥BC于H,
∵AD∥BC,DE∥AB,∴四边形ABED是平行四边形.
∴DE=AB=2,BE=AD=1,EC=4-1=3.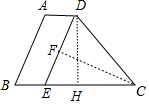
∴DC=EC.即△CDE为等腰三角形.
∵CF⊥ED,ED=2,
∴DF=1.∴CF=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$.
S△CDE=$\frac{1}{2}$CD•EF=$\frac{1}{2}$EC•DH,
即2×2$\sqrt{2}$=3×DH,
∴DH=$\frac{4\sqrt{2}}{3}$.
所以梯形面积=$\frac{1}{2}$×(1+4)×$\frac{4\sqrt{2}}{3}$=$\frac{10\sqrt{2}}{3}$.
故答案为$\frac{10\sqrt{2}}{3}$.
点评 本题考查了梯形,难度较大,因不知道各边长度,所以须先探究,确定图形的大致情形;求梯形高运用了等积法,这是解决有关高的问题时常用的方法.平移梯形的腰,把梯形转化为平行四边形和三角形,是解决梯形问题时常作的辅助线.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
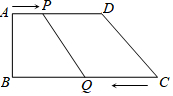 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24厘米,AB=8厘米,BC=30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24厘米,AB=8厘米,BC=30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
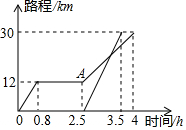 周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
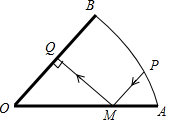 两面镜OA、OB如图放置,OA=OB=10cm,点P是$\widehat{AB}$上,PM为入射光线,且PM∥OB.
两面镜OA、OB如图放置,OA=OB=10cm,点P是$\widehat{AB}$上,PM为入射光线,且PM∥OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com