
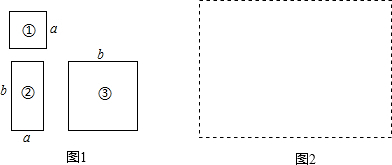
分析 (1)根据小正方形①1张,大正方形③2张,长方形②3张,直接画出图形,利用图形分解因式即可;
(2)由长方形②的周长为34,得出a+b=17,由题意可知:小正方形①与大正方形③的面积之和为a2+b2=169,将a+b=17两边同时平方,可求得ab的值,从而可求得长方形②的面积;
(3)设正方形的边长为(na+mb),其中(n、m为正整数)由完全平方公式可知:(na+mb)2=n2a2+2nmab+m2b2.因为现有三种纸片各8张,
n2≤8,m2≤8,2mn≤8(n、m为正整数)从而可知n≤2,m≤2,从而可得出答案.
解答 解:(1)如图: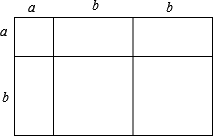
拼成边为(a+2b)和(a+b)的长方形
∴a2+3ab+2b2=(a+2b)(a+b);
(2)∵长方形②的周长为34,
∴a+b=17.
∵小正方形①与大正方形③的面积之和为169,
∴a2+b2=169.
将a+b=17两边同时平方得:(a+b)2=172,整理得:a2+2ab+b2=289,
∴2ab=289-169,
∴ab=60.
∴长方形②的面积为60.
(3)设正方形的边长为(na+mb),其中(n、m为正整数)
∴正方形的面积=(na+mb)2=n2a2+2nmab+m2b2.
∵现有三种纸片各8张,
∴n2≤8,m2≤8,2mn≤8(n、m为正整数)
∴n≤2,m≤2.
∴共有以下四种情况;
①n=1,m=1,正方形的边长为a+b;
②n=1,m=2,正方形的边长为a+2b;
③n=2,m=1,正方形的边长为2a+b;
④n=2,m=2,正方形的边长为2a+2b.
点评 此题考查因式分解的运用,要注意结合图形解决问题,解题的关键是灵活运用完全平方公式.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2800}{x}$-$\frac{2800}{5x}$=2 | B. | $\frac{2800}{5x}$-$\frac{2800}{x}$=2 | C. | $\frac{2800}{x}$-$\frac{2800}{4x}$=2 | D. | $\frac{2800}{4x}$-$\frac{2800}{x}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | 1或5 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
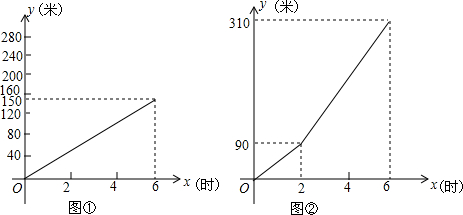
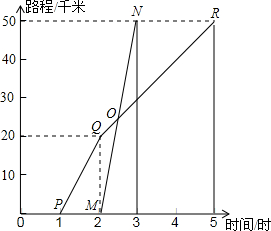 如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com