解:(1)在正方形ABCD中,AC与BD互相垂直平分,
∴AM=CM,AN=CN,
∴∠MAC=∠MCA,∠NAC=∠NCA,
∵∠CME=30°,∠CNF=50°,
∴∠MAC=

∠CME=15°,
∠NAC=

∠CNF=25°,
∴∠EAF=∠MAC+∠NAC=15°+25°=40°;

(2)如图,∠EAF′=90°+
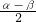
.
理由如下:在正方形ABCD中,AC与BD互相垂直平分,
∴AM=CM,AN′=CN′,
∴∠MAC=∠MCA,∠N′AC=∠N′CA,
∵∠CME=α,∠CN′F′=β,
∴∠MAC=

∠CME=

α,
∠N′AC=

(180°-β)=90°-

β,
∴∠EAF′=∠MAC+∠N′AC=

α+90°-

β=90°+
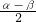
.
故答案为:90°+
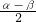
.
分析:(1)根据正方形的对角线互相垂直平分以及线段垂直平分线上的点到线段两端点的距离相等可得AM=CM,AN=CN,再根据等边对等角的性质可得∠MAC=∠MCA,∠NAC=∠NCA,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠MAC与∠NAC的度数,相加即可得解;
(2)根据正方形的对角线互相垂直平分以及线段垂直平分线上的点到线段两端点的距离相等可得AM=CM,AN′=CN′,再根据等边对等角的性质可得∠MAC=∠MCA,∠N′AC=∠N′CA,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠MAC,利用三角形的内角和等于180°求出∠N′AC,两者相加即可得解.
点评:本题考查了正方形的对角线互相垂直平分的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,综合性较强,但难度不是很大,熟练掌握各性质并理清各角度之间的关系是解题的关键.

 已知在正方形ABCD中,对角线AC、DB交于点O,E是CD边上一点,AE与对角线DB交于点M,连接CM.
已知在正方形ABCD中,对角线AC、DB交于点O,E是CD边上一点,AE与对角线DB交于点M,连接CM. ∠CME=15°,
∠CME=15°, ∠CNF=25°,
∠CNF=25°,
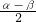 .
. ∠CME=
∠CME= α,
α, (180°-β)=90°-
(180°-β)=90°- β,
β, α+90°-
α+90°- β=90°+
β=90°+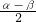 .
. .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案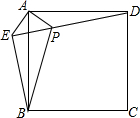 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=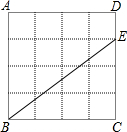 (2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.
(2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.