
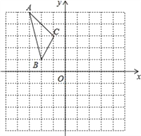
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
【答案】(1)点A1的坐标为(2,2),B1点的坐标为(3,﹣2);(2)A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);(3)△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);
【解析】试题分析:(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
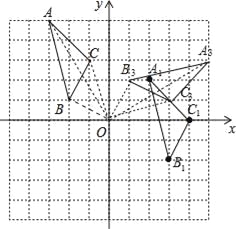
试题解析:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣20)+(+3)﹣(﹣5)﹣(+7)
(2)﹣ ![]() +
+ ![]() +
+ ![]() ﹣
﹣ ![]()
(3)(﹣ ![]() )×(﹣25)×(﹣1
)×(﹣25)×(﹣1 ![]() )×4
)×4
(4)(﹣1+ ![]() ﹣
﹣ ![]() +
+ ![]() )÷(﹣
)÷(﹣ ![]() )
)
(5)(﹣ ![]() )×(﹣
)×(﹣ ![]() )+(﹣
)+(﹣ ![]() )×(+
)×(+ ![]() )
)
(6)﹣14﹣(1﹣0.5)× ![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,
求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.


【拓展延伸】
(4)在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
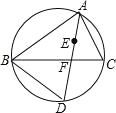
【题目】如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D.
(1)求证:∠BAD=∠CBD;
(2)求证:DE=DB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解古算题:今有共买物,人出八,赢三;人出七,不足四,问人数、物价几何?
题目大意是:几个人共同买一件物品,每人出8钱,余3钱;每人出7钱,缺4钱,求参与共同购物的有几人?物品价值多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月1日在北京天安门广场举行隆重的国庆70周年庆祝活动,在阅兵和群众游行活动中,共有约15万人参加.则15万用科学记数法表示为( )
A.1.5×10B.15×104C.1.5×105D.1.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
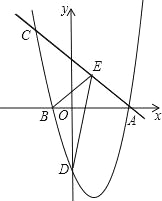
【题目】如图,抛物线y=![]() +bx﹣4(a≠0)与x轴交于A(4,0),B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
+bx﹣4(a≠0)与x轴交于A(4,0),B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式的变形中,不正确的是( )
A.若 x=y, 则 x+5=y+5
B.若 ![]() (a≠0),则x=y
(a≠0),则x=y
C.若-3x=-3y,则x=y
D.若mx=my,则x=y
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com