
【题目】如图,在△ ![]() 中,点
中,点 ![]() ,
, ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() ,
, ![]() 的中点,且
的中点,且 ![]() .
.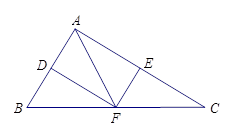
(1)求证:四边形 ![]() 为矩形;
为矩形;
(2)若 ![]() ,
, ![]() ,写出矩形
,写出矩形 ![]() 的周长.
的周长.
【答案】
(1)
证明:连接 ![]() .
.
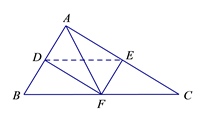
∵ ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() 的中点,
的中点,
∴ ![]() ,
, ![]() .
.
∵点 ![]() 是边
是边 ![]() 的中点,
的中点,
∴ ![]() .
.
∴ ![]()
∴四边形 ![]() 为平行四边形.
为平行四边形.
由点 ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() 的中点,可得:
的中点,可得:
![]() .
.
∵ ![]() ,
,
∴ ![]() ,即
,即 ![]() .
.
∴四边形 ![]() 为矩形.
为矩形.
(2)
解:由(1)知四边形ADFE为矩形,
∴ △ABC为RT△,且∠BAC=90°.
∵ F为BC中点,AF=2.
∴BC=4
又∵∠C=30° ,
∴AB=2,
∴AC=![]() =2
=2![]() .
.
∴![]()
【解析】(1)连接 D E,由D、 E 、 F 分别是中点,得到EF∥AD ,AD=EF,根据一组对边平行且相等的四边形为平行四边形. 再根据平行四边形的性质即与已知条件得DE=AF .根据对角线相等的平行四边形为矩形.
(2)由(1)知四边形ADFE为矩形,由矩形性质得△ABC为RT△,且∠BAC=90°.根据直角三角形斜边上的中线等于斜边的一半由AF=2得BC=4.再由∠C=30° ,得AB=2,由勾股定理得AC=![]() =2
=2![]() .从而求出四边形ADFE的周长。
.从而求出四边形ADFE的周长。![]()
【考点精析】根据题目的已知条件,利用三角形中位线定理和平行四边形的判定的相关知识可以得到问题的答案,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=10,点D , E , F分别是AB , BC , AC的中点,则四边形ADEF的周长为( ).
A.16
B.12
C.10
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某一天北京与上海的气温 ![]() (单位:
(单位: ![]() )随时间
)随时间 ![]() (单位:时)变化的图象.根据图中信息,下列说法错误的是( )
(单位:时)变化的图象.根据图中信息,下列说法错误的是( )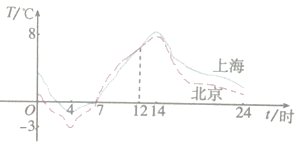
A.12时北京与上海的气温相同
B.从8时到11时,北京比上海的气温高
C.从4时到14时,北京、上海两地的气温逐渐升高
D.这一天中上海气温达到 ![]() 的时间大约在上午10时
的时间大约在上午10时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC,交AC于点E.把△ADE沿直线DE折叠,点A落在点A'处.连结BA',设AD=x,△ADE的边DE上的高为y.
(1) 求出y与x的函数关系式;
(2) 若以点A'、B、D为顶点的三角形与△ABC 相似,求x的值;
(3) 当x取何值时,△A' DB是直角三角形.
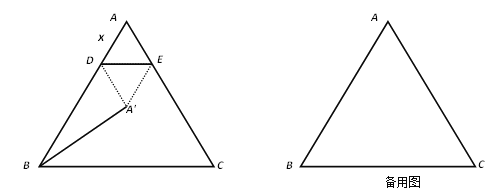
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表列出了国外几个城市与首都北京的时差(带正号的表示同一时刻比北京时间早的时数),如北京时间的上午10:00时,东京时间的10点已过去了1小时,现在已是10+1=11:00.

(1)如果现在是北京时间8:00,那么现在的纽约时间是多少;
(2)此时(北京时间8:00)小明想给远在巴黎姑妈打电话,你认为合适吗?为什么?
(3)如果现在是芝加哥时间上午6:00,那么现在北京时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
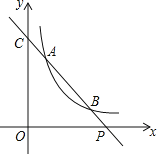
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com