
【题目】(1)特例求解:在△ABC中,若三角形的三边为6、8、10,则这个三角形的面积 为 .
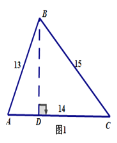
(2)一般化探究:在三角形ABC中,若AB=13,AC=14,BC=15,求△ABC的面积.
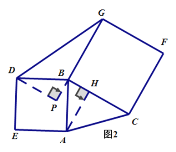
(3)模型建立:在图1三角形中,分别以AB,BC为边向外作正方形ABDE和正方形BCFG,试说明S△ABC=S△BDG.(温馨提示:作DP![]() BG,AH
BG,AH![]() BC)
BC)
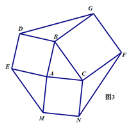
(4)模型应用:分别以图1中三角形的三边为边向外作正方形ABDE、正方形BCFG和正方形AMNC,如图3,利用(3)中的结论求多边形DEMNFG的面积,直接写出结论.
【答案】(1)24;(2)84;(3)见解析;(4)926.
【解析】
(1)先用勾股定理的逆定理判断三角形为直角三角形,再直接直角三角形面积公式求解;
(2)通过作一边上的高将一般三角形转化为直角三角形,利用勾股定理建立方程组计算,即可求解;
(3)先证明![]() ≌
≌![]() (AAS)得到DP=AH,再利用等底等高的三角形面积相等即可得证;
(AAS)得到DP=AH,再利用等底等高的三角形面积相等即可得证;
(4)利用(3)的结论得到![]() =
=![]() =
=![]() =
=![]() ,再结合正方形的面积公式得到多边形DEMNFG的面积=4
,再结合正方形的面积公式得到多边形DEMNFG的面积=4![]() +
+![]() +
+![]() +
+![]() ,从而得解.
,从而得解.
解:(1)∵![]() ,∴△ABC为直角三角形,∴
,∴△ABC为直角三角形,∴![]() ;
;
(2)如图

过点B作BD⊥AC交AC于D,
设AD=x,则DC=14-x,由勾股定理可得:
在直角三角形ADB中,![]() ,
,
在直角三角形BCD中,![]() ,
,
∴![]() ,
,
解得:x=5,
∴![]() ,
,
∴BD=12,
∴![]() ;
;
(3)如图

分别过点D、A作DP![]() BG,AH
BG,AH![]() BC交GB的延长线与P,交BC与H,
BC交GB的延长线与P,交BC与H,
∵∠DBA+∠ABC+∠CBG+∠DBG=360°,而∠DBA=∠CBG=90°,
∴∠ABC+∠DBG=180°,
又∵∠DBP+∠DBG=180°,
∴∠ABC=∠DBP,
在![]() 和
和![]() 中
中

∴![]() ≌
≌![]() (AAS),
(AAS),
∴DP=AH,
又∵![]() ,
,
![]() ,
,
而BC=BG,DP=AH,
∴![]() =
=![]() ;
;
(4)如图

由(3)的证明方法及结论可得:![]() =
=![]() =
=![]() =
=![]() ,
,
而![]() ,
,![]() ,
,![]() ,,
,,
∴多边形DEMNFG的面积=![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]()
=4![]() +
+![]() +
+![]() +
+![]() ,
,
=4×84+![]() +
+![]() +
+![]()
=926


科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABEF 的面积为 4,△BCE 是等边三角形,点 C 在正方形ABEF 外,在对角线 BF 上有一点 P,使 PC+PE 最小,则这个最小值的平方为( )
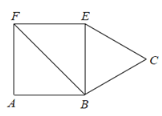
A.![]() B.
B.![]() C.12D.
C.12D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里吨),铁路运价为1元/(公里吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.
问:(1)这家食品厂到A地的距离是多少?
(2)这家食品厂此次买进的原料每吨5000元,卖出的食品每吨10000元,此批食品销售完后工厂共获利多少元?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
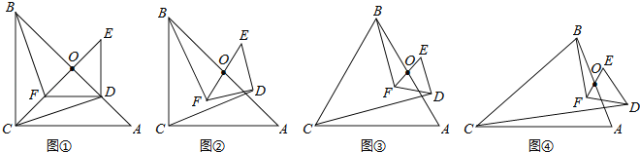
【题目】如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出![]() 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一长方形鸡场,鸡场的一边靠墙(墙长 18 米),另三边用竹篱笆围成,竹篱笆的总长为 35 米,与墙平行的边留有 1 米宽的门(门用其它材料做成),若鸡场的面积为 160 平方米,则鸡场与墙垂直的边长为( )

A.7.5 米B.8米C.10米D.10米或8米
查看答案和解析>>
科目:初中数学 来源: 题型:
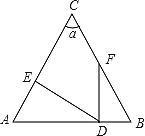
【题目】如图∠A=∠B,∠C=![]() ,DE⊥AC于点E,FD⊥AB于点D.
,DE⊥AC于点E,FD⊥AB于点D.
(1)若∠EDA=25°,则∠EDF=________°;
(2)若∠A=65°,则∠EDF=_______°;
(3)若![]() =50°,则∠EDF=_______°;
=50°,则∠EDF=_______°;
(4)若∠EDF=65°,则![]() _______°;
_______°;
(5)∠EDF与![]() 的关系为_______.
的关系为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组
(1)若a=2,请直接写出此时方程组的解;
(2)若方程组的解满足x+y=6,求a的值;
(3)若方程组的解x,y的值都为非负数,求2x-y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com