
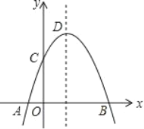
����Ŀ����ͼ��������y=��x2+2x+m+1��x���ڵ�A��a��0����B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ����⣺
�ٵ�x��0ʱ��y��0��
����a=��1����b=3��
����������������P��x1��y1����Q��x2��y2������x1��1��x2����x1+x2��2����y1��y2��
�ܵ�C���������߶Գ���ĶԳƵ�ΪE����G��F�ֱ���x���y���ϣ���m=2ʱ���ı���EDFG�ܳ�����СֵΪ6![]() ��
��
����������������____________��
���𰸡��ڢۣ�
��������
��1�����ݶ��κ����������ޣ��жϳ�y�ķ��ţ�
��2������A��B���ڶԳ���Գƣ����b��ֵ��
��3������![]() ����x1��1��x2���Ӷ��õ�Q�����Գ����Զ����ͼ�������жϳ�y1��y2��
����x1��1��x2���Ӷ��õ�Q�����Գ����Զ����ͼ�������жϳ�y1��y2��
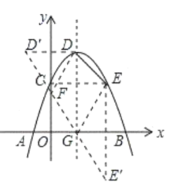
��4����D����y��ĶԳƵ�![]() ��E����x��ĶԳƵ�
��E����x��ĶԳƵ�![]() ������
������![]()
![]() ��DE��
��DE��![]()
![]() �ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ�����D��E��
�ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ�����D��E��![]() ��
��![]() �����꼴�ɽ��
�����꼴�ɽ��
��1����x��0ʱ������ͼ���һ�������ޣ���0<x<bʱ��y>0����x>bʱ��y<0���ʱ�ѡ�����
��2�����κ����Գ���Ϊx=-![]() =1����A��B����x=1�Գƣ���a=-1ʱ����
=1����A��B����x=1�Գƣ���a=-1ʱ����![]() =1�����b=3���ʱ�ѡ����ȷ��
=1�����b=3���ʱ�ѡ����ȷ��
��3����x1+x2��2��
��![]() ��
��
�֡�x1��1��x2��
��Q�����Գ����Զ��
������ͼ�����£�
��y1��y2���ʱ�ѡ����ȷ��
��4����ͼ����D����x��ĶԳƵ�![]() ��E����x��ĶԳƵ�
��E����x��ĶԳƵ�![]() ������
������![]()
![]() ��
��![]()
![]() �ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ��
�ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ��
��m=2ʱ�����κ���Ϊy=��x2+2x+3������������Ϊy=-1+2+3=4��DΪ��1��4������![]() Ϊ��-1��4����C������Ϊ��0��3������EΪ��2��3����
��-1��4����C��������0��3������E��2��3����![]() ��2��-3����DE=
��2��-3����DE=![]() ��
��![]()
![]() =
=![]() ��
��
���ı���EDFG�ܳ�����СֵΪ![]() ��
��
���ı���EDFG�ܳ�����СֵΪ![]() ���ʱ�ѡ�����
���ʱ�ѡ�����
�ʴ�Ϊ���ڢۣ�


 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ѧ��������������ijУ�ƻ���������ѡ�γ̣����֡��赸���鷨����Ӱ��Ҫ��ÿ��ѧ������ѡ����ֻ��ѡ��һ�ſγ̣�Ϊ��֤�ƻ�����Чʵʩ��ѧУ����Բ���ѧ��������һ�ε��飬�������˽�����Ƴ����²�������ͳ�Ʊ���ͳ��ͼ��
ѧ��ѡ�γ�ͳ�Ʊ�
�γ� | ���� | ��ռ�ٷֱ� |
���� | 14 |
|
�赸 | 8 |
|
�鷨 | 16 |
|
��Ӱ |
|
|
�ϼ� |
|
|

����������Ϣ������������⣺
��1��![]() ������
������![]() ������
������
��2�����![]() ��ֵ����ȫ����ͳ��ͼ��
��ֵ����ȫ����ͳ��ͼ��
��3����У��1500��ѧ�����������ѡ�ޡ����֡��γ̵�ѧ���ж�������
��4���ߣ�1������ߣ�2�������2��ѡ�ޡ��赸���γ������赸������ѧУ������4���������ȡ2�˱��š��赸���ڿ�����ʽ�ϱ��ݣ������б�������״ͼ�ķ���������ȡ��2��ǡ������ͬһ���༶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
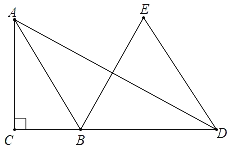
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬AB��![]() ��D��CB�ӳ�����һ�㣬��BDΪ���������ȱ�������EBD������AD����AD��11���ҡ�ABE��2��ADE����tan��ADE��ֵΪ_____��
��D��CB�ӳ�����һ�㣬��BDΪ���������ȱ�������EBD������AD����AD��11���ҡ�ABE��2��ADE����tan��ADE��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
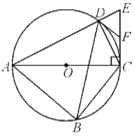
����Ŀ����ͼ���ı���![]() �ڽ���
�ڽ���![]() ���Խ���
���Խ���![]() Ϊ
Ϊ![]() ��ֱ��������
��ֱ��������![]() ��AC�Ĵ��߽�AD���ӳ����ڵ�E����FΪCE���е㣬����DB��DC��DF��
��AC�Ĵ��߽�AD���ӳ����ڵ�E����FΪCE���е㣬����DB��DC��DF��
��1����֤��DF��![]() �����ߣ�
�����ߣ�
��2����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��ͼ����
��ͼ����![]() ����
����![]() ������
������![]() ��
��![]() ����
����![]() ��
��
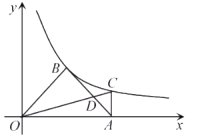
��1�����������Ľ���ʽ��
��2������![]() ��
��![]() �ᣬ������������
�ᣬ������������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
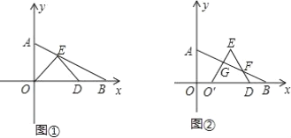
����Ŀ����ͼ����Rt��AOB�У���ABO=30����BO=4���ֱ���OA��OB�����ڵ�ֱ�߽���ƽ��ֱ������ϵ��D��Ϊx���������ϵ�һ�㣬��ODΪһ���ڵ�һ���������ȱߡ�ODE��
��1����ͼ�ٵ�E��ǡ�������߶�AB��ʱ����E�����ꣻ
��2������D��ԭ�������x���������ƶ������D��ԭ��ľ���Ϊx����ODE���AOB�ص����ֵ����Ϊy����E�㵽���AOB�����棬�ҵ�D�ڵ�B���ʱ��д��y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3���ڣ�1���ʵ������£�����ODE���߶�OB������ƽ����ͼ�ڣ�ͼ���Ƿ����һ�����߶�OO��ʼ����ȵ��߶Σ�������ڣ���ֱ��ָ�������߶Σ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
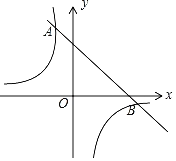
����Ŀ����ͼ��һ�κ���y��k1x+b��ͼ���뷴��������y��![]() ��ͼ���ཻ��A��B���㣬���е�A������Ϊ����1��4������B������Ϊ��4��n����
��ͼ���ཻ��A��B���㣬���е�A������Ϊ����1��4������B������Ϊ��4��n����
��1���������������ı���ʽ��
��2������ͼ��ֱ��д������k1x+b��![]() ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������й��Ŵ�����ѧר�������ij��ֱ�־�й��Ŵ���ѧ�γ�����������ϵ��������һ�����⣺�����ж�����һţ�۹�-�������֮�ۣ�һ������ţ�۲���һ�����ţ֮�ۣ���ţ�����۸����Σ��������Ϊ��������ƥ����һͷţ�ļ�Ǯ����һ�����IJ��������ǰ�ƥ���ļ�Ǯ��һƥ��������ͷţ�ļ�Ǯ��һ����IJ��������ǰ�ͷţ�ļ�Ǯ����һͷţ��һƥ��������Ǯ����һƥ��ֵ![]() Ǯ��һͷţֵ
Ǯ��һͷţֵ![]() Ǯ�����������ķ�����Ϊ�� ��
Ǯ�����������ķ�����Ϊ�� ��
A. B.
B.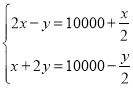
C.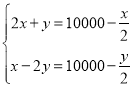 D.
D.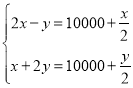
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() ��ֱ��
��ֱ��![]() ��y�ύ�ڵ�A����˫����
��y�ύ�ڵ�A����˫����![]() ���ڵ�
���ڵ�![]() ��
��
��1�����B�����꼰k��ֵ��
��2����ֱ��ABƽ�ƣ�ʹ����x�ύ�ڵ�C����y�ύ�ڵ�D����![]() �����Ϊ6����ֱ��CD�ı���ʽ��
�����Ϊ6����ֱ��CD�ı���ʽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com