

分析 (1)利用判定定理(SAS)可证;
(2)①利用(1)的结论与正方形的性质,只需证明∠FDE+∠DFG=90°即可;
②由DE⊥FG可构造直角三角形,利用等边三角形的性质及三角函数可求DE的长.
解答 (1)证明:∵四边形ABCD是正方形,AC是其对角线,
∴∠DCE=∠BCE,CD=CB
在△BCE与△DCE中,$\left\{\begin{array}{l}{CD=CB}&{(已证)}\\{∠DCE=∠BCE}&{(已证)}\\{CE=CE}&{(公共边)}\end{array}\right.$
∴△BCE≌△DCE(SAS).
(2)①证明:∵由(1)可知△BCE≌△DCE,
∴∠FDE=∠FBC
又∵四边形ABCD是正方形,
∴CD∥AB,
∴∠DFG=∠BGF,∠CFB=∠GBF,
又∵FG=FB,
∴∠FGB=∠FBG,
∴∠DFG=∠CFB,
又∵∠FCB=90°,
∴∠CFB+∠CBF=90°,
∴∠EDF+∠DFG=90°,
∴DE⊥FG
②解:如下图所示,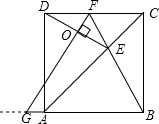
∵△BFG为等边三角形,
∴∠BFG=60°,
∵由(1)知∠DFG=∠CFB=60°,
在Rt△FCB中,∠FCB=90°,
∴FC=CB•cot60°=$\frac{2\sqrt{3}}{3}$,DF=2-$\frac{2\sqrt{3}}{3}$,
又∵DE⊥FG,
∴∠FDE=∠FED=30°,OD=OE,
在Rt△DFO中,
OD=DF•cos30°=$\sqrt{3}$-1,
∴DE=2($\sqrt{3}$-1)
点评 本题考查了正方形、等边三角形、直角三角形及三角函数等知识点,解题的关键是掌握三角形全等的判定定理、两直线垂直的条件及综合应用所学知识的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$-$\sqrt{3}$=1 | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{x}$×$\sqrt{y}$=xy |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四边形中至多有一个角是钝角或直角 | |
| B. | 四边形中至少有两个角是钝角或直角 | |
| C. | 四边形中四个角都是钝角或直角 | |
| D. | 四边形中没有一个角是钝角或直角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这1000名考生是总体的一个样本 | B. | 近8000名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 1000名学生是样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-5<b-5 | B. | 2+a<2+b | C. | 3a>3b | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$.
已知:如图,在△ABC中,AB=BC=2,∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).△ABC关于y轴对称的△A′B′C′;则以A、B、B′、A′为顶点的四边形的面积7$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com