Question

14．给定复杂几何条件下求点的坐标．
（1）已知点A（1，2），P在x轴上，且∠APO=45°，直接写出P点坐标；
（2）已知点A（1，2），P在x轴上，且△APO面积是4，直接写出P点坐标；
（3）已知点A（0，1），B（2，0），AB⊥PB，AB=PB，直接写出P点坐标；
（4）已知点A（2，0），B（0，1），P在第一象限，AB=PB，AB⊥PB，直接写出P点坐标．

Answer 1

分析 （1）作AD⊥x轴于D，易证得△PAD是等腰直角三角形，得出AD=PD=2，从而求得P的坐标；
（2）由三角形面积求得OP=4，从而求得P的坐标；
（3）作PD⊥x轴于D，易证得△AOB≌△BDP，得出OA=BD=1，OB=PD=2，从而求得P的坐标；
（3）作PD⊥y轴于D，易证得△AOB≌△BDP，得出OA=BD=2，OB=PD=1，从而求得P的坐标．

解答 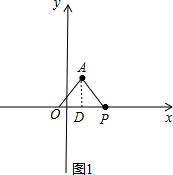解：（1）如图1，作AD⊥x轴于D，
∵∠APO=45°，
∴∠DAP=45°，
∴AD=PD，
∵A（1，2），
∴OD=1，AD=2，
∴PD=2，
∴P（3，0）或（-1，0）；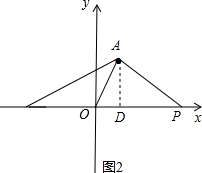
（2）如图2，∵A（1，2），
∴OD=1，AD=2，
∵△APO面积是4，
∴$\frac{1}{2}$OP•AD=4，
∴OP=4，
∴P（4，0）或（-4，0）；
（3）如图3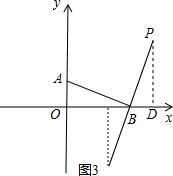，作PD⊥x轴于D，
∵AB⊥PB，
∴∠ABO+∠PBD=90°，
∵∠ABO+∠BAO=90°，
∴∠BAO=∠PBD，
在△AOB和△BDP中
$\left\{\begin{array}{l}{∠BAO=∠PBD}\\{∠AOB=∠BDP=90°}\\{AB=PB}\end{array}\right.$
∴△AOB≌△BDP（AAS），
∴OA=BD，OB=PD，
∵A（0，1），B（2，0），
∴BD=1，PD=2，
∴P（3，2）或（1，2）；
（4）如图4，作PD⊥y轴于D，
∵AB⊥PB，
∴∠ABO+∠PBD=90°，
∵∠ABO+∠BAO=90°，
∴∠BAO=∠PBD，
在△AOB和△BDP中
$\left\{\begin{array}{l}{∠BAO=∠PBD}\\{∠AOB=∠BDP=90°}\\{AB=PB}\end{array}\right.$
∴△AOB≌△BDP（AAS），
∴OA=BD，OB=PD，
∵A（2，0），B（0，1），
∴BD=2，PD=1，
∴P（1，3）或（-1，-1）．

点评 本题考查了等腰直角三角形的判定和性质、三角形全等的判定和性质，坐标与图形性质的综合运用，注意分类讨论思想的运用．