
 如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0°<α<360°),则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α=60°或180°或300°.
如图,正方形ABCD与正方形AEFG起始时互相重合,现将正方形AEFG绕点A逆时针旋转,设旋转角∠BAE=α(0°<α<360°),则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α=60°或180°或300°. 分析 分点F在BD上和点F在AC上两种情况考虑:①当点F在BD上时,设正方形ABCD的边长为2a,根据正方形的性质可得出AO和AF的长,在通过解直角三角形可得出∠OAF=60°,进而可得出α的值;②由点C、A、F三点共线,可得出B、A、E三点共线,由此得出∠BAE=180°.综上即可得出结论.
解答 解:依照题意画出图形,如图所示.
①当点F在BD上时:令AC、BD的交点为O,设正方形ABCD的边长为2a,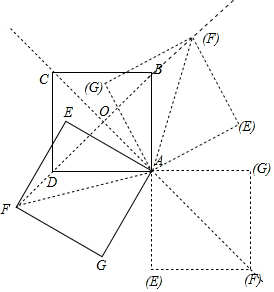
则AC=AF=2$\sqrt{2}$a,AO=$\frac{1}{2}$AC=$\sqrt{2}$a.
∵四边形ABCD为正方形,
∴AC⊥BD,∠BAC=∠DAC=∠EAF=45°,
∴∠AOF=90°.
在Rt△AOF中,AO=$\sqrt{2}$a,AF=2$\sqrt{2}$a,
∴cos∠OAF=$\frac{AO}{AF}$=$\frac{1}{2}$,
∴∠OAF=60°,
∴α=∠OAF=60°或α=360°-∠OAF=300°;
②当点F在AC上时,
∵C、A、F三点共线,∠EAF=∠BAC=45°,
∴B、A、E三点共线,
∴α=∠BAE=180°.
综上可知:当正方形的顶点F落在正方形的对角线AC或BD所在直线上时,α=60°或180°.
故答案为:60°或180°或300°.
点评 本题考查了旋转的性质以及正方形的性质,解题的关键是分点F在BD上和点F在AC上两种情况考虑.本题属于中档题,难度不大,解决该题型题目时,利用旋转的性质找出相等的边角关系是关键.


科目:初中数学 来源: 题型:解答题
 如图,一架长为AB=12米的云梯斜靠在一面墙上,且∠BAC=30°,设AB的中点为点P,现将梯子沿水平线向右滑动,使∠EDC=45°,设ED的中点为点Q,求点P运动到点Q时,所经过的路径的长.
如图,一架长为AB=12米的云梯斜靠在一面墙上,且∠BAC=30°,设AB的中点为点P,现将梯子沿水平线向右滑动,使∠EDC=45°,设ED的中点为点Q,求点P运动到点Q时,所经过的路径的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形OMNP是由正方形ABCD经过平移和旋转得到的,O是正方形ABCD的旋转中心;那么将△BOE绕点O按逆时针方向旋转90°后,点E与点F重合.如果正方形的面积是4cm2,那么四边形OEBF的面积等于1cm2.
如图,正方形OMNP是由正方形ABCD经过平移和旋转得到的,O是正方形ABCD的旋转中心;那么将△BOE绕点O按逆时针方向旋转90°后,点E与点F重合.如果正方形的面积是4cm2,那么四边形OEBF的面积等于1cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,三角形ABC沿BC边所在的直线向左平移得到三角形DEF,下列说法错误的是( )
如图,三角形ABC沿BC边所在的直线向左平移得到三角形DEF,下列说法错误的是( )| A. | DE∥AB | B. | ∠D=∠A | C. | AC=DF | D. | ∠D=∠DEF |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知A($2\sqrt{3}$,2)、B($2\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2$\sqrt{2}$,2$\sqrt{2}$)的位置,则图中阴影部分的面积为$\frac{7}{8}π$.
如图,已知A($2\sqrt{3}$,2)、B($2\sqrt{3}$,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2$\sqrt{2}$,2$\sqrt{2}$)的位置,则图中阴影部分的面积为$\frac{7}{8}π$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 过平行四边形纸片的一个顶点作一条线段,沿这条线段剪下一个三角形纸片,将它平移到右边的位置,可得到新的平行四边形.
过平行四边形纸片的一个顶点作一条线段,沿这条线段剪下一个三角形纸片,将它平移到右边的位置,可得到新的平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相较于点M,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.
如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相较于点M,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com