
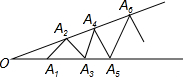
 如图,已知点A1、A2、A3、A4…是∠O两边上的点,且O A1=A1 A2=A2 A3=A3 A4=A4 A5=…,从左向右数,恰好只能作出4个等腰三角形,请问∠O=18°.
如图,已知点A1、A2、A3、A4…是∠O两边上的点,且O A1=A1 A2=A2 A3=A3 A4=A4 A5=…,从左向右数,恰好只能作出4个等腰三角形,请问∠O=18°.  夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知正方形ABCD,顶点A与坐标原点重合,顶点B、D分别在x轴和y轴的正半轴上,顶点C在反比例函数y=$\frac{16}{x}$(x>0)的图象上,如图所示,动点P以每秒1个单位的速度从A点出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
已知正方形ABCD,顶点A与坐标原点重合,顶点B、D分别在x轴和y轴的正半轴上,顶点C在反比例函数y=$\frac{16}{x}$(x>0)的图象上,如图所示,动点P以每秒1个单位的速度从A点出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com