
 直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运
直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运
 动到点A,过点D作x轴的垂线,分别交直线 和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
动到点A,过点D作x轴的垂线,分别交直线 和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒) (1)求点A,B,C的坐标; (2)若点 正好在△PQR的某边上,求t的值;
(1)求点A,B,C的坐标; (2)若点 正好在△PQR的某边上,求t的值; 
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
 ,
, 是一次函数
是一次函数 的图像和反比例函数
的图像和反比例函数 的图像的
的图像的
 与
与 轴的交点
轴的交点 的坐标及三角形
的坐标及三角形 的面积.
的面积. 为何值时,一次函数的值小于反比例函数的值?
为何值时,一次函数的值小于反比例函数的值?查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
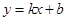 (k>0)和x轴上,已知点B1(1,1),B2(3,2), 则Bn的坐标是_______
(k>0)和x轴上,已知点B1(1,1),B2(3,2), 则Bn的坐标是_______
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 和一次函数
和一次函数 的图象相交于第一象限内的点A,且点A的横坐标为1. 过点A作AB⊥x轴于点B,△AOB的面积为1.
的图象相交于第一象限内的点A,且点A的横坐标为1. 过点A作AB⊥x轴于点B,△AOB的面积为1.
 的图象与x轴相交于点C,求∠ACO的度数;
的图象与x轴相交于点C,求∠ACO的度数; >
> >0 时,x的取值范围.
>0 时,x的取值范围. 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (亩)与补贴数额
(亩)与补贴数额 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系.随着补贴数额 的不断增大,出口量也不断增加,但每亩蔬菜的收益
的不断增大,出口量也不断增加,但每亩蔬菜的收益 (元)会相应降低,且
(元)会相应降低,且 与
与 之间也大致满足如图2所示的一次函数关系.
之间也大致满足如图2所示的一次函数关系.
 和每亩蔬菜的收益
和每亩蔬菜的收益 与政府补贴数额
与政府补贴数额 之间的函数关系式;
之间的函数关系式; (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额 定为多少?并求出总收益
定为多少?并求出总收益 的最大值.
的最大值.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(30,30) | B.(﹣8 ,8 ,8 ) ) | C.(﹣4 ,4 ,4 ) ) | D.(4 ,﹣4 ,﹣4 ) ) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com