
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a=﹣![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.

【答案】(1)①D的坐标是(3,1),抛物线的解析式为y=﹣![]() x2+
x2+![]() x;②在抛物线上是否存在点P(
x;②在抛物线上是否存在点P(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),使得∠POB与∠BCD互余;(2)a的值为a=
),使得∠POB与∠BCD互余;(2)a的值为a=![]() .
.
【解析】
试题分析: (1)①过点D作DF⊥x轴于点F,先通过三角形全等求得D的坐标,把D的坐标和a=﹣![]() ,c=0代入y=ax2+bx+c即可求得抛物线的解析式;②先证得CD∥x轴,进而求得要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,设P的坐标为(x,﹣
,c=0代入y=ax2+bx+c即可求得抛物线的解析式;②先证得CD∥x轴,进而求得要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,设P的坐标为(x,﹣ ![]() x2+
x2+![]() x),分两种情况讨论即可求得;(2)若符合条件的Q点的个数是3个,根据tan∠QOB=tan∠BAO=
x),分两种情况讨论即可求得;(2)若符合条件的Q点的个数是3个,根据tan∠QOB=tan∠BAO=![]() =
=![]() ,得到直线OQ的解析式为y=﹣
,得到直线OQ的解析式为y=﹣![]() x,要使直线OQ与抛物线y=ax2+bx+c有一个交点,所以方程ax2﹣4ax+3a+1=﹣
x,要使直线OQ与抛物线y=ax2+bx+c有一个交点,所以方程ax2﹣4ax+3a+1=﹣![]() x有两个相等的实数根,所以△=(﹣4a+
x有两个相等的实数根,所以△=(﹣4a+![]() )2﹣4a(3a+1)=0,即4a2﹣8a+
)2﹣4a(3a+1)=0,即4a2﹣8a+![]() =0,解得a=
=0,解得a=![]() ,根据实际情况对a进行取值即可.
,根据实际情况对a进行取值即可.
试题解析:(1)①过点D作DF⊥x轴于点F,如图1,
∵∠DBF+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠DBF=∠BAO,
又∵∠AOB=∠BFD=90°,AB=BD,
∴△AOB≌△BFD(AAS)
∴DF=BO=1,BF=AO=2,
∴D的坐标是(3,1),
根据题意,得a=﹣![]() ,c=0,且a×32+b×3+c=1,
,c=0,且a×32+b×3+c=1,
∴b=![]() ,
,
∴该抛物线的解析式为y=﹣![]() x2+
x2+![]() x;
x;
②∵点A(0,2),B(1,0),点C为线段AB的中点,
∴C(![]() ,1),
,1),
∵C、D两点的纵坐标都为1,
∴CD∥x轴,
∴∠BCD=∠ABO,
∴∠BAO与∠BCD互余,
要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,
设P的坐标为(x,﹣![]() x2+
x2+![]() x),
x),
(Ⅰ)当P在x轴的上方时,过P作PG⊥x轴于点G,如图2,
则tan∠POB=tan∠BAO,即![]() =
=![]() ,
,
∴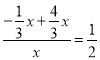 ,解得x1=0(舍去),x2=
,解得x1=0(舍去),x2=![]() ,
,
∴﹣![]() x2+
x2+![]() x=
x=![]() ,
,
∴P点的坐标为(![]() ,
,![]() );
);
(Ⅱ)当P在x轴的下方时,过P作PG⊥x轴于点G,如图3
则tan∠POB=tan∠BAO,即![]() =
=![]() ,
,
∴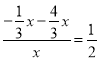 ,解得x1=0(舍去),x2=
,解得x1=0(舍去),x2=![]() ,
,
∴﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() ,
,
∴P点的坐标为(![]() ,﹣
,﹣![]() );
);
综上,在抛物线上是否存在点P(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),使得∠POB与∠BCD互余.
),使得∠POB与∠BCD互余.
(2)如图3,∵D(3,1),E(1,1),
抛物线y=ax2+bx+c过点E、D,代入可得![]() ,解得
,解得![]() ,
,
所以y=ax2﹣4ax+3a+1.
分两种情况:
①当抛物线y=ax2+bx+c开口向下时,若满足∠QOB与∠BCD互余且符合条件的Q点的个数不可能是3个
②当抛物线y=ax2+bx+c开口向上时,
(i)当点Q在x轴的上方时,直线OQ与抛物线y=ax2+bx+c必有两个交点,符合条件的点Q必定有2个;
(ii)当点Q在x轴的下方时,要使直线OQ与抛物线y=ax2+bx+c只有1个交点,才能使符合条件的点Q共3个.
根据(2)可知,要使得∠QOB与∠BCD互余,则必须∠QOB=∠BAO,
∴tan∠QOB=tan∠BAO=![]() =
=![]() ,此时直线OQ的解析式为y=﹣
,此时直线OQ的解析式为y=﹣![]() x,要使直线OQ与抛物线y=ax2+bx+c有一个交点,所以方程ax2﹣4ax+3a+1=﹣
x,要使直线OQ与抛物线y=ax2+bx+c有一个交点,所以方程ax2﹣4ax+3a+1=﹣![]() x有两个相等的实数根,所以△=(﹣4a+
x有两个相等的实数根,所以△=(﹣4a+![]() )2﹣4a(3a+1)=0,即4a2﹣8a+
)2﹣4a(3a+1)=0,即4a2﹣8a+![]() =0,解得a=
=0,解得a=![]() ,
,
∵抛物线的顶点在x轴下方
∴![]() <0,
<0,
∴a>1,
∴a=![]() 舍去
舍去
综上所述,a的值为a=![]() .
.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的集合里.
![]() ,π,3.1415926,﹣0.456,3.030030003…(相邻的两个3之间0的个数逐渐增加),0,
,π,3.1415926,﹣0.456,3.030030003…(相邻的两个3之间0的个数逐渐增加),0, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
有理数集合:{ };
无理数集合:{ };
正实数集合:{ };
整数集合:{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为参加2019年“岳阳市初中毕业生升学体育考试”,小明同学进行了刻苦的练习,在测试跳绳时,记录下5次一分钟所跳次数的成绩(单位:次)分别为:180,185,185,186,188.这组数据的众数、中位数依次是( )
A. 185,185B. 185,185.5C. 186,186D. 188,185.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是2010年11月份的日历,现用一长方形在日历表中任意框出4个数(如图2),下列表示a,b,c,d之间关系的式子中不正确的是( ) 
A.a+d=b+c
B.a﹣d=b﹣c
C.a+c+2=b+d
D.a+b+14=c+d
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门. ![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽查了10名同学的语文成绩,以80分为基准,超出的记为正数,不足的记为负数,记录的结果如下:﹣3、+12、﹣10、+8、﹣7、﹣3、﹣8、+1、0、+10
(1)这10名同学的最高分是 分,最低分是 分
(2)求这10名同学的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0. ![]()
(1)求点C表示的数;
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,若AP+BQ=2PQ,求时间t;
(3)若点P从A向右运动,点M为AP中点,在P点到达点B之前:① ![]() 的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com