
【题目】问题提出
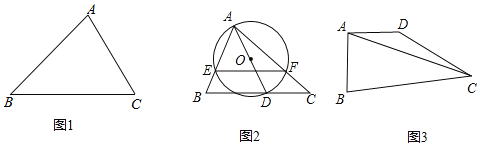
(1)如图1,在△ABC中,∠A=75°,∠C=60°,AC=6![]() ,求△ABC的外接圆半径R的值;
,求△ABC的外接圆半径R的值;
问题探究
(2)如图2,在△ABC中,∠BAC=60°,∠C=45°,AC=8![]() ,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
问题解决
(3)如图3,在四边形ABCD中,∠BAD=90°,∠BCD=30°,AB=AD,BC+CD=12![]() ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
【答案】(1)△ABC的外接圆的R为6;(2)EF的最小值为12;(3)存在,AC的最小值为9![]() .
.
【解析】
(1)如图1中,作△ABC的外接圆,连接OA,OC.证明∠AOC=90°即可解决问题;
(2)如图2中,作AH⊥BC于H.当直径AD的值一定时,EF的值也确定,根据垂线段最短可知当AD与AH重合时,AD的值最短,此时EF的值也最短;
(3)如图3中,将△ADC绕点A顺时针旋转90°得到△ABE,连接EC,作EH⊥CB交CB的延长线于H,设BE=CD=x.证明EC=![]() AC,构建二次函数求出EC的最小值即可解决问题.
AC,构建二次函数求出EC的最小值即可解决问题.
解:(1)如图1中,作△ABC的外接圆,连接OA,OC.

∵∠B=180°﹣∠BAC﹣∠ACB=180°﹣75°﹣60°=45°,
又∵∠AOC=2∠B,
∴∠AOC=90°,
∴AC=6![]() ,
,
∴OA=OC=6,
∴△ABC的外接圆的R为6.
(2)如图2中,作AH⊥BC于H.
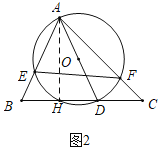
∵AC=8![]() ,∠C=45°,
,∠C=45°,
∴AH=ACsin45°=8![]() ×
×![]() =8
=8![]() ,
,
∵∠BAC=60°,
∴当直径AD的值一定时,EF的值也确定,
根据垂线段最短可知当AD与AH重合时,AD的值最短,此时EF的值也最短,
如图2﹣1中,当AD⊥BC时,作OH⊥EF于H,连接OE,OF.
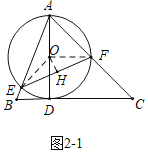
∵∠EOF=2∠BAC=120°,OE=OF,OH⊥EF,
∴EH=HF,∠OEF=∠OFE=30°,
∴EH=OFcos30°=4![]()
![]() =6,
=6,
∴EF=2EH=12,
∴EF的最小值为12.
(3)如图3中,将△ADC绕点A顺时针旋转90°得到△ABE,连接EC,作EH⊥CB交CB的延长线于Hspan>,设BE=CD=x.

∵∠AE=AC,∠CAE=90°,
∴EC=![]() AC,∠AEC=∠ACE=45°,
AC,∠AEC=∠ACE=45°,
∴EC的值最小时,AC的值最小,
∵∠BCD=∠ACB+∠ACD=∠ACB+∠AEB=30°,
∴∠∠BEC+∠BCE=60°,
∴∠EBC=120°,
∴∠EBH=60°,
∴∠BEH=30°,
∴BH=![]() x,EH=
x,EH=![]() x,
x,
∵CD+BC=12![]() ,CD=x,
,CD=x,
∴BC=12![]() ﹣x
﹣x
∴EC2=EH2+CH2=(![]() x)2+
x)2+![]() =x2﹣12
=x2﹣12![]() x+432,
x+432,
∵a=1>0,
∴当x=﹣![]() =6
=6![]() 时,EC的长最小,
时,EC的长最小,
此时EC=18,
∴AC=![]() EC=9
EC=9![]() ,
,
∴AC的最小值为9![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)根据图象,求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,问销售单价应定为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
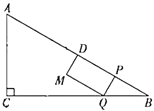
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.动点
的中点.动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位向终点
个单位向终点![]() 匀速运动(点
匀速运动(点![]() 不与
不与![]() 、
、![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() .以
.以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)直接写出![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边上时,求
的边上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形不是矩形时,求
重叠部分图形不是矩形时,求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(4)沿直线![]() 将矩形
将矩形![]() 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
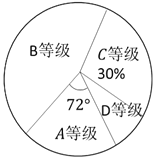
【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查了部分学生的数学成绩,并将抽样的数据进行了如下整理.
(1)填空![]() _______,
_______,![]() _______,数学成绩的中位数所在的等级_________.
_______,数学成绩的中位数所在的等级_________.
(2)如果该校有1200名学生参加了本次模拟测,估计![]() 等级的人数;
等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A级学生的数学成绩的平均分数.
①如下分数段整理样本
等级等级 | 分数段 | 各组总分 | 人数 |
|
|
| 4 |
|
| 843 |
|
|
| 574 |
|
|
| 171 | 2 |
②根据上表绘制扇形统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名工人分别加工a个同种零件.甲先加工一段时间,由于机器故障进行维修后继续按原来的工作效率进行加工,当甲加工![]() 小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
(1)甲的工作效率为 个/时,维修机器用了 小时
(2)乙的工作效率是 个/时;问题解决:
①乙加工多长时间与甲加工的零件数量相同,并求此时乙加工零件的个数;
②若乙比甲早10分钟完成任务,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
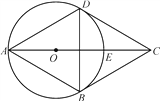
【题目】已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.
(1)判断⊙O与BC的位置关系,并说明理由;
(2)若CE=2,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号)
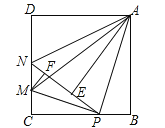
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为![]() ;
;
⑤当△ABP≌△ADN时,BP=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年2月16日,由著名导演林超贤的电影《红海行动》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定谁去看电影,规则如下:在一个不透明的袋子中装有编号1~4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出两数和的所有可能的结果;
(2)分别求出小亮和小丽获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com