
| A. | ($\sqrt{a}$)2=a | B. | 若a>b(ab≠0),则$\frac{1}{a}$<$\frac{1}{b}$ | ||
| C. | |a|•|b|=|ab| | D. | 若m为整数,则(m+$\frac{1}{2}$)2+$\frac{7}{4}$是整数 |
分析 根据事件发生的可能性大小判断相应事件的类型即可.
解答 解:A、($\sqrt{a}$)2=a是必然事件,故A不符合题意;
B、若a>b>0时(ab≠0),则$\frac{1}{a}$<$\frac{1}{b}$,a>0>b时,$\frac{1}{a}$>$\frac{1}{b}$,是随机事件,故B符合题意;
C、|a|•|b|=|ab是必然事件,故C不符合题意;
D、若m为整数,则(m+$\frac{1}{2}$)2+$\frac{7}{4}$=m2+m+2是整数是必然事件,故D不符合题意;
故选:B.
点评 本题考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
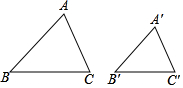 如图,用计算机或图形计算器画△ABC和△A′B′C′,使得∠A和∠A′都等于给定的∠α,∠B和∠B′都等于给定的∠β,那么∠C和∠C′相等吗?对应边的比$\frac{AC}{A′C′}$,$\frac{AB}{A′B′}$,$\frac{BC}{B′C′}$相等吗?这样的两个三角形相似吗?
如图,用计算机或图形计算器画△ABC和△A′B′C′,使得∠A和∠A′都等于给定的∠α,∠B和∠B′都等于给定的∠β,那么∠C和∠C′相等吗?对应边的比$\frac{AC}{A′C′}$,$\frac{AB}{A′B′}$,$\frac{BC}{B′C′}$相等吗?这样的两个三角形相似吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
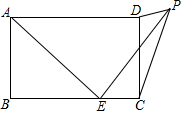 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长3或$\frac{7+\sqrt{17}}{4}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长3或$\frac{7+\sqrt{17}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com