
【题目】(1)方法选择
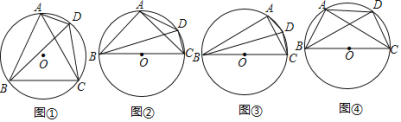
如图①,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .
.
小颖认为可用截长法证明:在![]() 上截取
上截取![]() ,连接
,连接![]() …
…
小军认为可用补短法证明:延长![]() 至点
至点![]() ,使得
,使得![]() …
…
请你选择一种方法证明.
(2)类比探究
(探究1)
如图②,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() .试用等式表示线段
.试用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(探究2)
如图③,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
(3)拓展猜想
如图④,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
【答案】(1)方法选择:证明见解析;(2)【探究1】:![]() ;【探究2】
;【探究2】![]() ;(3)拓展猜想:
;(3)拓展猜想:![]() .
.
【解析】
(1)方法选择:根据等边三角形的性质得到∠ACB=∠ABC=60°,如图①,在BD上截取DM=AD,连接AM,由圆周角定理得到∠ADB=∠ACB=60°,得到AM=AD,根据全等三角形的性质得到BM=CD,于是得到结论;
(2)类比探究:如图②,由BC是⊙O的直径,得到∠BAC=90°,根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,过A作AM⊥AD交BD于M,推出△ADM是等腰直角三角形,求得DM=![]() AD根据全等三角形的性质得到结论;
AD根据全等三角形的性质得到结论;
【探究2】
如图③,根据圆周角定理和三角形的内角和得到∠BAC=90°,∠ACB=60°,过A作AM⊥AD交BD于M,求得∠AMD=30°,根据直角三角形的性质得到MD=2AD,根据相似三角形的性质得到BM=![]() CD,于是得到结论;
CD,于是得到结论;
(3)如图④,由BC是⊙O的直径,得到∠BAC=90°,过A作AM⊥AD交BD于M,求得∠MAD=90°,根据相似三角形的性质得到BM=![]() CD,DM=
CD,DM=![]() AD,于是得到结论.
AD,于是得到结论.
(1)方法选择:∵![]() ,
,
∴![]() ,
,
如图①,在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)类比探究:如图②,
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
[探究2]如图③,∵若![]() 是
是![]() 的直径,
的直径,![]() ,
,
∴![]() ,
,![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
故答案为![]() ;
;
(3)拓展猜想:![]() ;
;
理由:如图④,∵若![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=x+b与x轴交于点A(﹣2,0),与y轴交于点B.双曲线y![]() 与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
(1)求点B的坐标;
(2)当点P的横坐标为2时,求k的值;
(3)连接PO,记△POB的面积为S.若![]() ,结合函数图象,直接写出k的取值范围.
,结合函数图象,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,点
,点![]() 在直线
在直线![]() 上,以点
上,以点![]() 为圆心,适当长度为半径画弧,分别交直线
为圆心,适当长度为半径画弧,分别交直线![]() ,
,![]() 于
于![]() ,
,![]() 两点,以点
两点,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与前弧交于点
长为半径画弧,与前弧交于点![]() (不与点
(不与点![]() 重合),连接
重合),连接![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() 交
交![]() 于点
于点![]() .若
.若![]() ,则下列结论错误的是( )
,则下列结论错误的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现如图1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交于点
交于点![]() .填空:①
.填空:①![]() 的值为______;②
的值为______;②![]() 的度数为______.
的度数为______.
(2)类比探究如图2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数,并说明理由;
的度数,并说明理由;
(3)拓展延伸在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线交于点
所在直线交于点![]() ,若
,若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 在同一条直线上时
在同一条直线上时![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
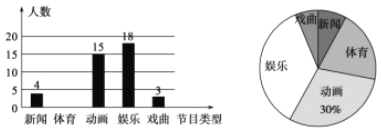
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
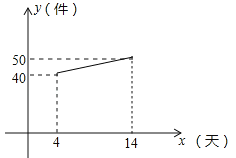
【题目】宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系: ![]() .
.
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
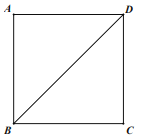
【题目】在正方形ABCD中,E是CD边上的点,过点E作EF⊥BD于F.
(1)尺规作图:在图中求作点E,使得EF=EC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接FC,求∠BCF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校七年级学生每周上网的时间,甲、乙两名学生进行了抽样调查.甲同学调查了七年级电脑爱好者中40名学生每周上网的时间;乙同学从全校800名七年级学生中随机抽取了40名学生,调查了每周上网的时间.甲、乙同学各自整理的样本数据如表:
上网时间t(小时/周) | 甲学生抽样人数(人) | 乙学生抽样人数(人) |
0≤t<1.5 | 6 | 22 |
1.5≤t<2.5 | 10 | 10 |
2.5≤t<3.5 | 16 | 6 |
t≥3.5 | 8 | 2 |
(1)你认为哪名学生抽取的样本不合理,请说明理由.
(2)请你根据抽取样本合理的学生的数据,将调查结果绘制成合适的统计图(绘制一种即可).
(3)专家建议每周上网2.5小时以上(含2.5小时)的学生应适当减少上网的时间,估计该校全体七年级学生中应适当减少上网的时间的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com