
【题目】如图,小华用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有( )个棋子.

A.159B.169C.172D.132
【答案】B
【解析】
观察图象得到第1个图案中有黑子1个,白子0个,共1个棋子;第2个图案中黑子有1个,白子6个,共1+6=7个棋子;第3个图案中黑子有1+2×6=13个,白子6个,共1+2×6+6=1+3×6=19个棋子;第4个图案中黑子有1+2×6=13个,白子有6+3×6=24个,共1+6×6=37个棋子;…,据此规律可得.
解:第1个图案中有黑子1个,白子0个,共1个棋子;
第2个图案中黑子有1个,白子6个,共1+6=7个棋子;
第3个图案中黑子有1+2×6=13个,白子6个,共1+2×6+6=1+3×6=19个棋子,
第4个图案中黑子有1+2×6=13个,白子有6+3×6=24个,共1+6×6=37个棋子;
…
第7个图案中黑子有1+2×6+4×6+6×6=73个,白子有6+3×6+5×6=54个,共1+21×6=127个棋子;
第8个图案中黑子有1+2×6+4×6+6×6=73个,白子有6+3×6+5×6+7×6=96个,共1+28×6=169个棋子;
故选:B.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)第一版=____%,“第四版”对应扇形的圆心角为________°;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为 . 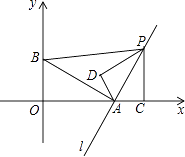
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 的
的![]() 所对边分别是
所对边分别是![]() ,且
,且![]() ,若满足
,若满足![]() ,则称
,则称![]() 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.
(1)若![]() ,判断
,判断![]() 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
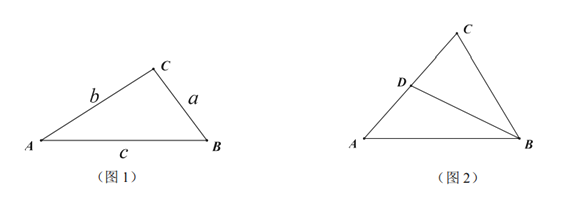
(3)如图2,在奇异三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,连结
边上的中点,连结![]() ,
,![]() 将
将![]() 分割成2个三角形,其中
分割成2个三角形,其中![]() 是奇异三角形,
是奇异三角形,![]() 是以
是以![]() 为底的等腰三角形,求
为底的等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).

(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知多项式3m3n2![]() 2mn3
2mn3![]() 2中,四次项的系数为a,多项式的次数为b,常数项为c,且4b、
2中,四次项的系数为a,多项式的次数为b,常数项为c,且4b、![]() 10c3、
10c3、![]() (a+b)2bc的值分别是点A、B、C在数轴上对应的数,点P从原点O出发,沿OC方向以1单位/s的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动(点P、Q分别运动到点C、O时停止运动),两点同时出发.
(a+b)2bc的值分别是点A、B、C在数轴上对应的数,点P从原点O出发,沿OC方向以1单位/s的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动(点P、Q分别运动到点C、O时停止运动),两点同时出发.
(1)分别求4b、![]() 10c3、
10c3、![]() (a+b)2bc的值;
(a+b)2bc的值;
(2)若点Q运动速度为3单位/s,经过多长时间P、Q两点相距70;
(3)当点P运动到线段AB上时,分别取OP和AB的中点E、F,试问![]() 的值是否变化,若变化,求出其范围:若不变,求出其值.
的值是否变化,若变化,求出其范围:若不变,求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设武术、舞蹈、剪纸三项活动课程,为了了解学生对这三项活动课程的兴趣情况,随机抽取了部分学生进行调查(每人从中只能选一顶),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.

(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是___;
(3)在扇形统计图中,计算女生喜欢剪纸活动课程人数对应的圆心角度数;
(4)已知该校有1200名学生,请结合数据简要分析该校学生对剪纸课程的兴趣情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD,△BCE,△ACF,请解答下列问题:
(1)求证:四边形AFED是平行四边形;
(2)当△ABC满足 时,四边形AFED是矩形.
当△ABC满足 时,四边形AFED是菱形.
当△ABC满足 时,四边形AFED是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com