
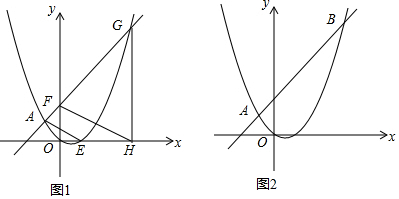
·ÖĪö £Ø1£©øł¾ŻµćA”¢BµÄ×ų±źĄūÓĆ“ż¶ØĻµŹż·Ø£¬¼“æÉĒó³öÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©øł¾ŻµćA”¢FµÄ×ų±źĄūÓĆ“ż¶ØĻµŹż·Ø£¬æÉĒó³öÖ±ĻßAFµÄ½āĪöŹ½£¬ĮŖĮ¢Ö±ĻßAFŗĶÅ×ĪļĻߵĽāĪöŹ½³É·½³Ģ×飬Ķعż½ā·½³Ģ×éæÉĒó³öµćGµÄ×ų±ź£¬½ų¶ųæÉµĆ³öµćHµÄ×ų±ź£¬ĄūÓĆ·Ö½āŅņŹ½·Ø½«Å×ĪļĻß½āĪöŹ½±äŠĪĪŖ½»µćŹ½£¬ÓÉ“ĖæÉµĆ³öµćEµÄ×ų±ź£¬ŌŁøł¾ŻµćA”¢E£ØF”¢H£©µÄ×ų±źĄūÓĆ“ż¶ØĻµŹż·Ø£¬æÉĒó³öÖ±ĻßAE£ØFH£©µÄ½āĪöŹ½£¬ÓÉ“ĖæÉÖ¤³öFH”ĪAE£»
£Ø3£©øł¾ŻµćA”¢BµÄ×ų±źĄūÓĆ“ż¶ØĻµŹż·Ø£¬æÉĒó³öÖ±ĻßABµÄ½āĪöŹ½£¬½ų¶ųæÉÕŅ³öµćP”¢QµÄ×ų±ź£¬·ÖµćMŌŚĻ߶ĪPQÉĻŅŌ¼°µćMŌŚĻ߶ĪQPµÄŃÓ³¤ĻßÉĻĮ½ÖÖĒéæöæ¼ĀĒ£¬½čÖśĻąĖĘČż½ĒŠĪµÄŠŌÖŹæÉµĆ³öµćMµÄ×ų±ź£¬ŌŁĄūÓƶž“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷æÉµĆ³ö¹ŲÓŚtµÄŅ»ŌŖ¶ž“Ī·½³Ģ£¬½āÖ®¼“æÉµĆ³ö½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©½«µćA£Ø-1£¬1£©”¢B£Ø4£¬6£©“śČėy=ax2+bxÖŠ£¬
$\left\{\begin{array}{l}{a-b=1}\\{16a+4b=6}\end{array}\right.$£¬½āµĆ£ŗ$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=$\frac{1}{2}$x2-$\frac{1}{2}$x£®
£Ø2£©Ö¤Ć÷£ŗÉčÖ±ĻßAFµÄ½āĪöŹ½ĪŖy=kx+m£¬
½«µćA£Ø-1£¬1£©“śČėy=kx+mÖŠ£¬¼“-k+m=1£¬
”ąk=m-1£¬
”ąÖ±ĻßAFµÄ½āĪöŹ½ĪŖy=£Øm-1£©x+m£®
ĮŖĮ¢Ö±ĻßAFŗĶÅ×ĪļĻß½āĪöŹ½³É·½³Ģ×飬
$\left\{\begin{array}{l}{y=£Øm-1£©x+m}\\{y=\frac{1}{2}{x}^{2}-\frac{1}{2}x}\end{array}\right.$£¬½āµĆ£ŗ$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=1}\end{array}\right.$£¬$\left\{\begin{array}{l}{{x}_{2}=2m}\\{{y}_{2}=2{m}^{2}-m}\end{array}\right.$£¬
”ąµćGµÄ×ų±źĪŖ£Ø2m£¬2m2-m£©£®
”ßGH”ĶxÖį£¬
”ąµćHµÄ×ų±źĪŖ£Ø2m£¬0£©£®
”ßÅ×ĪļĻߵĽāĪöŹ½ĪŖy=$\frac{1}{2}$x2-$\frac{1}{2}$x=$\frac{1}{2}$x£Øx-1£©£¬
”ąµćEµÄ×ų±źĪŖ£Ø1£¬0£©£®
ÉčÖ±ĻßAEµÄ½āĪöŹ½ĪŖy=k1x+b1£¬
½«A£Ø-1£¬1£©”¢E£Ø1£¬0£©“śČėy=k1x+b1ÖŠ£¬
$\left\{\begin{array}{l}{-{k}_{1}+{b}_{1}=1}\\{{k}_{1}+{b}_{1}=0}\end{array}\right.$£¬½āµĆ£ŗ$\left\{\begin{array}{l}{{k}_{1}=-\frac{1}{2}}\\{{b}_{1}=\frac{1}{2}}\end{array}\right.$£¬
”ąÖ±ĻßAEµÄ½āĪöŹ½ĪŖy=-$\frac{1}{2}$x+$\frac{1}{2}$£®
ÉčÖ±ĻßFHµÄ½āĪöŹ½ĪŖy=k2x+b2£¬
½«F£Ø0£¬m£©”¢H£Ø2m£¬0£©“śČėy=k2x+b2ÖŠ£¬
$\left\{\begin{array}{l}{{b}_{2}=m}\\{2m{k}_{2}+{b}_{2}=0}\end{array}\right.$£¬½āµĆ£ŗ$\left\{\begin{array}{l}{{k}_{2}=-\frac{1}{2}}\\{{b}_{2}=m}\end{array}\right.$£¬
”ąÖ±ĻßFHµÄ½āĪöŹ½ĪŖy=-$\frac{1}{2}$x+m£®
”ąFH”ĪAE£®
£Ø3£©ÉčÖ±ĻßABµÄ½āĪöŹ½ĪŖy=k0x+b0£¬
½«A£Ø-1£¬1£©”¢B£Ø4£¬6£©“śČėy=k0x+b0ÖŠ£¬
$\left\{\begin{array}{l}{{-k}_{0}+{b}_{0}=1}\\{4{k}_{0}+{b}_{0}=6}\end{array}\right.$£¬½āµĆ£ŗ$\left\{\begin{array}{l}{{k}_{0}=1}\\{{b}_{0}=2}\end{array}\right.$£¬
”ąÖ±ĻßABµÄ½āĪöŹ½ĪŖy=x+2£®
µ±ŌĖ¶ÆŹ±¼äĪŖtĆėŹ±£¬µćPµÄ×ų±źĪŖ£Øt-2£¬t£©£¬µćQµÄ×ų±źĪŖ£Øt£¬0£©£®
µ±µćMŌŚĻ߶ĪPQÉĻŹ±£¬¹żµćP×÷PP”ä”ĶxÖįÓŚµćP”䣬¹żµćM×÷MM”ä”ĶxÖįÓŚµćM”䣬Ōņ”÷PQP”ä”×”÷MQM”䣬ČēĶ¼2ĖłŹ¾£®
”ßQM=2PM£¬
”ą$\frac{QM”ä}{QP”ä}$=$\frac{MM”ä}{PP”ä}$=$\frac{2}{3}$£¬
”ąQM”ä=$\frac{4}{3}$£¬MM”ä=$\frac{2}{3}$t£¬
”ąµćMµÄ×ų±źĪŖ£Øt-$\frac{4}{3}$£¬$\frac{2}{3}$t£©£®
Ó֔ߵćMŌŚÅ×ĪļĻßy=$\frac{1}{2}$x2-$\frac{1}{2}$xÉĻ£¬
”ą$\frac{2}{3}$t=$\frac{1}{2}$”Į£Øt-$\frac{4}{3}$£©2-$\frac{1}{2}$£Øt-$\frac{4}{3}$£©£¬
½āµĆ£ŗt=$\frac{15”Ą\sqrt{113}}{6}$£»
µ±µćMŌŚĻ߶ĪQPµÄŃÓ³¤ĻßÉĻŹ±£¬
Ķ¬ĄķæÉµĆ³öµćMµÄ×ų±źĪŖ£Øt-4£¬2t£©£¬
”ßµćMŌŚÅ×ĪļĻßy=$\frac{1}{2}$x2-$\frac{1}{2}$xÉĻ£¬
”ą2t=$\frac{1}{2}$”Į£Øt-4£©2-$\frac{1}{2}$£Øt-4£©£¬
½āµĆ£ŗt=$\frac{13”Ą\sqrt{89}}{2}$£®
×ŪÉĻĖłŹö£ŗµ±ŌĖ¶ÆŹ±¼äĪŖ$\frac{15-\sqrt{113}}{6}$Ćė”¢$\frac{15+\sqrt{113}}{6}$Ćė”¢$\frac{13-\sqrt{89}}{2}$Ćė»ņ$\frac{13+\sqrt{89}}{2}$ĆėŹ±£¬QM=2PM£®
µćĘĄ ±¾Ģāæ¼²éĮĖ“ż¶ØĻµŹż·ØĒóŅ»“Ī£Ø¶ž“Ī£©ŗÆŹż½āĪöŹ½”¢¶ž“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷”¢¶ž“ĪŗÆŹżµÄČżÖÖŠĪŹ½”¢ĻąĖĘČż½ĒŠĪµÄŠŌÖŹŅŌ¼°Į½ĢõÖ±ĻßĻą½»»ņĘ½ŠŠ£¬½āĢāµÄ¹Ų¼üŹĒ£ŗ£Ø1£©øł¾ŻµćA”¢BµÄ×ų±źĄūÓĆ“ż¶ØĻµŹż·Ø£¬Ēó³öÅ×ĪļĻߵĽāĪöŹ½£»£Ø2£©øł¾ŻµćA”¢E£ØF”¢H£©µÄ×ų±źĄūÓĆ“ż¶ØĻµŹż·Ø£¬Ēó³öÖ±ĻßAE£ØFH£©µÄ½āĪöŹ½£ŗ£Ø3£©·ÖµćMŌŚĻ߶ĪPQÉĻŅŌ¼°µćMŌŚĻ߶ĪQPµÄŃÓ³¤ĻßÉĻĮ½ÖÖĒéæö£¬½čÖśĻąĖĘČż½ĒŠĪµÄŠŌÖŹÕŅ³öµćMµÄ×ų±ź£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻABC=90”ć£¬AB=12£¬BC=5£¬ČōDEŹĒ”÷ABCµÄÖŠĪ»Ļߣ¬ŃÓ³¤DE½»”÷ABCµÄĶā½Ē”ĻACMµÄĘ½·ÖĻßÓŚµćF£¬ŌņĻ߶ĪDFµÄ³¤ĪŖ£Ø””””£©
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻABC=90”ć£¬AB=12£¬BC=5£¬ČōDEŹĒ”÷ABCµÄÖŠĪ»Ļߣ¬ŃÓ³¤DE½»”÷ABCµÄĶā½Ē”ĻACMµÄĘ½·ÖĻßÓŚµćF£¬ŌņĻ߶ĪDFµÄ³¤ĪŖ£Ø””””£©| A£® | 9 | B£® | 10 | C£® | 12 | D£® | 13 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | m=$\frac{5}{3}$ | B£® | m=3 | C£® | m=$\frac{5}{3}$»ņ1 | D£® | m=$\frac{5}{3}$»ņ3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
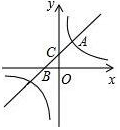 ČēĶ¼£¬Ö±Ļßy=x+bÓėĖ«ĒśĻßy=$\frac{k}{x}$£ØkĪŖ³£Źż£¬k”Ł0£©ŌŚµŚŅ»ĻóĻŽÄŚ½»ÓŚµćA£Ø1£¬2£©£¬ĒŅÓėxÖį”¢yÖį·Ö±š½»ÓŚB£¬CĮ½µć£®
ČēĶ¼£¬Ö±Ļßy=x+bÓėĖ«ĒśĻßy=$\frac{k}{x}$£ØkĪŖ³£Źż£¬k”Ł0£©ŌŚµŚŅ»ĻóĻŽÄŚ½»ÓŚµćA£Ø1£¬2£©£¬ĒŅÓėxÖį”¢yÖį·Ö±š½»ÓŚB£¬CĮ½µć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŅŃÖŖABŹĒ”ŃOµÄÖ±¾¶£¬CDÓė”ŃOĻąĒŠÓŚC£¬BE”ĪCO£®
ČēĶ¼£¬ŅŃÖŖABŹĒ”ŃOµÄÖ±¾¶£¬CDÓė”ŃOĻąĒŠÓŚC£¬BE”ĪCO£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
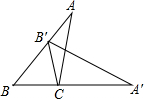 ČēĶ¼£¬½«”÷ABCČʵćCĖ³Ź±ÕėŠż×Ŗ£¬Ź¹µćBĀäŌŚAB±ßÉĻµćB”䓦£¬“ĖŹ±£¬µćAµÄ¶ŌÓ¦µćA”äĒ”ŗĆĀäŌŚBC±ßµÄŃÓ³¤ĻßÉĻ£¬ĻĀĮŠ½įĀŪ“ķĪóµÄŹĒ£Ø””””£©
ČēĶ¼£¬½«”÷ABCČʵćCĖ³Ź±ÕėŠż×Ŗ£¬Ź¹µćBĀäŌŚAB±ßÉĻµćB”䓦£¬“ĖŹ±£¬µćAµÄ¶ŌÓ¦µćA”äĒ”ŗĆĀäŌŚBC±ßµÄŃÓ³¤ĻßÉĻ£¬ĻĀĮŠ½įĀŪ“ķĪóµÄŹĒ£Ø””””£©| A£® | ”ĻBCB”ä=”ĻACA”ä | B£® | ”ĻACB=2”ĻB | C£® | ”ĻB”äCA=”ĻB”äAC | D£® | B”äCĘ½·Ö”ĻBB”äA”ä |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com