
���� �������и����������г�����x�IJ���ʽ�飬���x��ȡֵ��Χ���ɣ�
��� �⣺ԭ��ʽ����ʽ�ɻ�Ϊ��$\left\{\begin{array}{l}2x-1��0\\ 3x+3��0\end{array}\right.$����$\left\{\begin{array}{l}2x-1��0\\ 3x+3��0\end{array}\right.$��
����ʽ����⣻
�ⲻ��ʽ��ڵã�-1��x����$\frac{1}{2}$��
�ʲ���ʽ��Ľ⼯Ϊ��-1��x����$\frac{1}{2}$��
���� ���⿼����ǽ�һԪһ�β���ʽ�飬����ͬ����������������������������ø����г�����x�IJ���ʽ���ǽ�����Ĺؼ���


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ۼ�x��Ԫ/ǧ�ˣ� | �� | 50 | 60 | 70 | 80 | �� |
| ������y��ǧ�ˣ� | �� | 100 | 90 | 80 | 70 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-1 | B�� | -1��x��2 | C�� | x��2 | D�� | x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
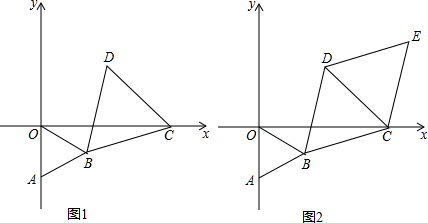
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������ȵ�ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | ֻ��һ��ʵ���� | D�� | û��ʵ���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com