
����Ŀ����֪������ABCD�У�AB��4cm��BC��8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
��1����ͼ��1��������AF��CE��
���ı���AFCE��ʲô�����ı��Σ�˵�����ɣ�
����AF�ij���
��2����ͼ��2��������P��Q�ֱ��A��C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У���֪��P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬��A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��

���𰸡���1�� �����Σ����ɼ���������AF��5����2�� ![]() �룮
�룮
��������
��1������֤���ı���ABCDΪƽ���ı��Σ��ٸ��ݶԽ����ഹֱƽ�ֵ�ƽ���ı��������������ж���
�ڸ��ݹ��ɶ���������AF�ij���
��2����������ۿ�֪��P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴�ɣ�
��1���١��ı���ABCD�Ǿ��Σ�
��AD��BC��
���CAD����ACB����AEF����CFE��
��EF��ֱƽ��AC��
��OA��OC��
�ڡ�AOE�͡�COF�У�
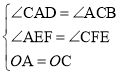
���AOE�ա�COF(AAS)��
��OE��OF(AAS)��
��EF��AC��
���ı���AFCEΪ���Σ�
�������εı߳�AF��CF��xcm����BF��(8��x)cm��
��Rt��ABF�У�AB��4cm���ɹ��ɶ�������
16+(8��x)2��x2��
��ã�x��5��
��AF��5��
��2������ͼ����֪����P��AF��ʱ��Q��CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
ͬ��P��AB��ʱ��Q��DE��CE�ϣ�Ҳ���ܹ���ƽ���ı��Σ�
��ֻ�е�P����BF�ϣ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��
��PC��QA��
�ߵ�P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC��5t��QA��12��4t��
��5t��12��4t��
��ã�t��![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��t��![]() �룮
�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,AC=BC,��C=90��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AB������ΪE.��֤��AB=AC+CD.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����
����![]() ������
������![]() �ϣ�
�ϣ�![]() ��
��

��1����ͼ 1����![]() ����
����![]() �Ķ�����
�Ķ�����
��2������![]() �㡱��Ϊ��
�㡱��Ϊ��![]() ��������
��������![]() ������
������![]() ƽ�ƣ��õ�
ƽ�ƣ��õ�![]() �������������䣨�� ͼ 2 ��ʾ����̽��
�������������䣨�� ͼ 2 ��ʾ����̽��![]() ��������ϵ��
��������ϵ��
��3���ڣ�2���������£���![]() ������Ϊ
������Ϊ![]() ����
����![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ���ڵ�
���ڵ�![]() ����
����![]() �� �ú� �� ��ʽ�ӱ�ʾ
�� �ú� �� ��ʽ�ӱ�ʾ![]() ��ֱ��д���𰸣���
��ֱ��д���𰸣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ�ӡ�����������顱����ί�ظ���ͨ��ijƫԶѧУ��һ��ȫ��Ϊ1200 �ĵ�·�����˸������������·�森����400 ����Ϊ�˾�����ɵ�·����������ÿ��Ĺ���Ч�ʱ�ԭ�ƻ����25%���������13����ɵ�·����������
��1����ԭ�ƻ�ÿ������·���������
��2�����а���ԭ��ÿ��֧�����˹���Ϊ1500Ԫ����߹���Ч�ʺ�ÿ��֧�������˵Ĺ���������20%������������̺�а��̹�֧�����˹��ʶ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��DC���е㣬����AE�����ӳ���BC���ӳ����ڵ�F��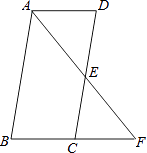
��1����֤����ADE�͡�CEF�������ȣ�
��2����AB=2AD����˵��AFǡ���ǡ�BAD��ƽ���ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���������ε�������ƽ���߽���һ�㣬������Ϊ�����ε����ģ�����������Բ��Բ�ģ������ڹ涨������ı��ε��ĸ��ǵĽ�ƽ���߽���һ�㣬���ǰ������Ҳ��Ϊ���ı��ε����ġ���
��1���Ծٳ�һ�������ĵ��ı��Σ�
��2����ͼ1����֪��O���ı���ABCD�����ģ���֤��AB+CD=AD+BC��
��3����ͼ2��Rt��ABC�У���C=90�㣮O�ǡ�ABC�����ģ���ֱ��DE�ر�AC��BC�ڵ�D��E����O��Ȼ���ı���ABED�����ģ�������ֱ��DE�ɻ�������������ͼ2�л���һ������������ֱ��DE������˵��������
��4�����⣨3���У���AC=3��BC=4������������һ��ֱ��DE��AB����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
1�����㡢![]() +��
+��![]() ����1��4tan45�� 2�� �ⷽ�̣�x2=3x��
����1��4tan45�� 2�� �ⷽ�̣�x2=3x��
��1�����㣺 ![]() +��
+�� ![]() ����1��4tan45��
����1��4tan45��
��2���ⷽ�̣�x2=3x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��C��D���ڡ�O�ϣ���C����CA��BD��OD���ӳ����ڵ�A������BC����B=��A=30�㣬BD=2 ![]() ��
��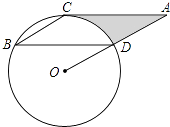
��1����֤��AC�ǡ�O�����ߣ�
��2�������߶�AC��AD�뻡CD��Χ�ɵ���Ӱ���ֵ����������������У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ���ı���![]() �У�
�У�![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ����һ�㣬��
����һ�㣬��![]() Ϊ����ƽ���ı���
Ϊ����ƽ���ı���![]() ����
����![]() ��Сֵ��__________��
��Сֵ��__________��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com