
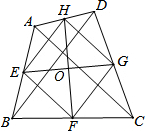
 如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.
如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.分析 (1)根据三角形的中位线定理和菱形的判定,可得顺次连接对角线相等的四边形各边中点所得四边形是菱形;
(2)根据菱形的性质得到EG⊥HF,且EG=2OE,FH=2OH,在Rt△OEH中,根据勾股定理得到OE2+OH2=EH2=4,再根据等式的性质,在等式的两边同时乘以4,根据4=22,把等式进行变形,并把EG=2OE,FH=2OH代入变形后的等式中,即可求出EG2+FH2的值.
解答 (1)证明:∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知,EH=FG=$\frac{1}{2}$BD,EF=HG=$\frac{1}{2}$AC,
又∵AC=BD,
∴EH=FG=EF=HG,
∴四边形EFGH是菱形;
(2)解:由(1)知,四边形EFGH是菱形,则EG⊥FH,EG=2OE,FH=2OH,
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH2=4,
等式两边同时乘以4得:4OE2+4OH2=4×4=16,
∴(2OE)2+(2OH)2=16,
即EG2+FH2=16.
点评 此题主要考查了三角形中位线定理和菱形的判定方法,题目比较典型,又有综合性,难度不大.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
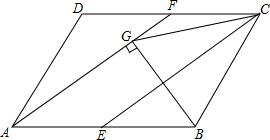 如图,E、F分别为平行四边形ABCD中AB、CD的中点,BG⊥AF于G,
如图,E、F分别为平行四边形ABCD中AB、CD的中点,BG⊥AF于G,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
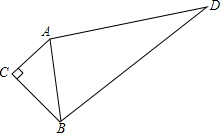 如图,∠C=90°,AC=3,BC=4,AD=12,BD=13.
如图,∠C=90°,AC=3,BC=4,AD=12,BD=13.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com