
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0)、B(1,0),与y轴交于点C(0,-4),P是直线AC下方抛物线上的点,若△ACP的面积为6,则tan∠AOP的值为_____________

【答案】6或![]() .
.
【解析】
连接PA,PC,过P作PD⊥x轴,与AC交于点E,采用待定系数法求出二次函数与直线AC的解析式,设出P点坐标,求出E点纵坐标,然后采用“铅锤法”表示出△ACP的面积,解方程求出P点坐标,再根据正切的定义即可求解.
如图,连接PA,PC,过P作PD⊥x轴,与AC交于点E,

将A(-4,0),B(1,0),C(0,-4)代入抛物线解析式得,
 ,解得
,解得
∴二次函数解析式为![]()
设直线AC解析式为![]() ,
,
将A(-4,0),C(0,-4)代入直线解析式得
![]() ,解得
,解得![]()
∴直线AC解析式为![]()
设P点坐标为![]() ,
,
∵PD⊥x轴,
∴E点横坐标为m,
将E点横坐标代入直线AC得![]() ,则E点坐标为
,则E点坐标为![]() ,
,
∴PE=![]()
∴S△ACP=![]() ,
,
解得![]() 或
或![]()
当m=-1时,P点坐标为(-1,-6),tan∠AOP=![]()
当m=-3时,P点坐标为(-3,-4),tan∠AOP=![]()
故答案为:6或![]() .
.


科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种款式童装,一天可售出30套,每套盈利40元.为了扩大销售,增加盈利,商场决定采取降价措施.若一套童装每降价1元,平均每天可多售出2套,设每套童装降价![]() 元时,商场一天可获利润
元时,商场一天可获利润![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)若要商场每天盈利1500元,则应降价多少元?
(3)当每套童装降价多少元时,商场可获最大利润?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖北省十堰市,第24题,10分)已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中,∠BAO=90°,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.

(1)如图1,若点B在OP上,则:
①AC OE(填“<”,“=”或“>”);
②线段CA、CO、CD满足的等量关系式是 ;
(2)将图1中的等腰Rt△ABO绕O点顺时针旋转α(0°<α<45°),如图2,那么(1)中的结论②是否成立?请说明理由;
(3)将图1中的等腰Rt△ABO绕O点顺时针旋转α(45°<α<90°),请你在图3中画出图形,并直接写出线段CA、CO、CD满足的等量关系式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OC2=OA·OB.

(1)证明:tan∠BAC· tan∠ABC=1;
(2)若点C的坐标为(0,2),tan∠OCB=2,
①求该抛物线的表达式;
②若点D是该抛物线上的一点,且位于直线BC上方,当四边形ABDC的面积最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
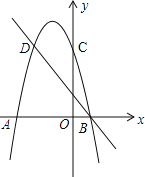
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
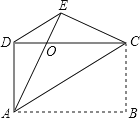
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com