科目：初中数学 来源：初中数学 三点一测丛书 八年级数学 下 （江苏版课标本） 江苏版 题型：013
反比例函数y＝
(k≠0)任取一点M(a，b)，过M作MA⊥x轴，MB⊥y轴，所得矩形OAMB的面积为S＝MA·MB＝|b|·|a|＝|ab|．又因为b＝
，故ab＝k，所以S＝|k|(如图(1))．
这就是说，过双曲线上任意一点作x轴、y轴的垂线，所得的矩形面积为|k|．这就是k的几何意义，会给解题带来方便．现举例如下：
例1：如(2)图，已知点P1(x1，y1)和P2(x2，y2)都在反比例函数y＝
(k＜0)的图像上，试比较矩形P1AOB与矩形P2COD的面积大小．
解答：
＝|k|
＝|k|
故＝
例2：如图(3)，在y＝
(x＞0)的图像上有三点A、B、C，经过三点分别向x轴引垂线，交x轴于A1、B1、C1三点，连结OA、OB、OC，记△OAA1、△OBB1、△OCC1的面积分别为S1、S2、S3，则有( )
A．S1＝S2＝S3
B．S1＜S2＜S3
C．S3＜S1＜S2
D．S1＞S2＞S3
解答：∵
＝
|k|＝，
＝|k|＝
＝|k|＝
S1＝S2＝S3，故选A．
例3：一个反比例函数在第三象限的图像如图(4)所示，若A是图像任意一点，AM⊥x轴，垂足为M，O是原点，如果△AOM的面积是3，那么这个反比例函数的解析式是________．
解答：∵S△AOM＝
|k|
又S△AOM＝3，
∴|k|＝3，|k|＝6
∴k＝±6
又∵曲线在第三象限
∴k＞0∴k＝6
∴所以反比例函数的解析式为y＝
．
根据是述意义，请你解答下题：
如图(5)，过反比例函数y＝
(x＞0)的图像上任意两点A、B分别作轴和垂线，垂足分别为C、D，连结OA、OB，设AC与OB的交点为E，△AOE与梯形ECDB的面积分别为S1、S2，比较它们的大小，可得
A．S1＞S2
B．S1＝S2
C．S1＜S2
D．大小关系不能确定
查看答案和解析>>
科目：初中数学 来源： 题型：047
我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等
(1)阅读与证明：
对于这两个三角形均为直角三角形，显然它们全等．
对于这两个三角形均为钝角三角形，可证它们全等(证明略)．
对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
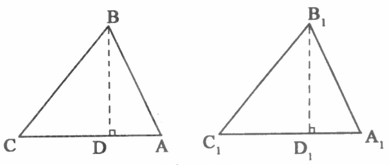
已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1Cl，∠C=∠Cl．
求证：△ABC≌△A1B1C1．
(请你将下列证明过程补充完整．)
证明：分别过点B，B1作BD⊥CA于D，B1 D1⊥C1 A1于D1.
则∠BDC=∠B1D1C1=900，
∵BC=B1C1，∠C=∠C1，
∴△BCD≌△B1C1D1，-
∴BD=B1D1．
(2)归纳与叙述：
由(1)可得到一个正确结论，请你写出这个结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则a:b=
，则
的值为
，则
＝＿＿＿＿．