
某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.(假设年租金的增加额均为5000元的整数倍)该公司要为租出的商铺每间每年交各种费用2万元,未租出的商铺每间每年交各种费用1万元.
(1)当每间商铺的年租金定为12万元时,能租出多少间?年收益多少万元?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益最大,最大值为多少?
(1)26,256;(2)当每间商铺的年租金定为13万元时,该公司的年收益最大,最大值为258万元.
解析试题分析:(1)判断出租出商铺的间数是解决本题的易错点.由题意可知:租出的房间数=30-增加了多少个5000元;年收益=租出去的商铺的收益-未租出的商铺的费用;根据以上两个数量关系列式解答即可.
设每间商铺的年租金为x万元,该公司的年收益为y万元,由(1)中年收益的计算方法列出函数关系式并化为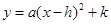 的形式,从而根据二次函数的性质就可以判断出年收益的最值.
的形式,从而根据二次函数的性质就可以判断出年收益的最值.
试题解析:
解:(1)租出间数为: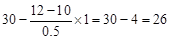 (间),
(间),
年收益为: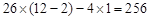 (万元).
(万元).
(2)设每间商铺的年租金为x万元,该公司的年收益为y万元,依题意,得: 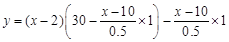
整理得: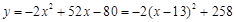
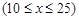
∴当 时,y有最大值为258,
时,y有最大值为258,
答:当每间商铺的年租金定为13万元时,该公司的年收益最大,最大值为258万元.
考点:二次函数的应用.


科目:初中数学 来源: 题型:解答题
如图,已知二次函数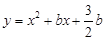 的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
的图象与x轴交于A、B两点(B在A的左侧),顶点为C, 点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
(1)求此二次函数的解析式和点C的坐标;
(2)当点D的坐标为(1,1)时,连接BD、 .求证:
.求证: 平分
平分 ;
;
(3)点G在抛物线的对称轴上且位于第一象限,若以A、C、G为顶点的三角形与以G、D、E为顶点的三角形相似,求点E的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知△ABC的三个顶点坐标分别为A(-4,0),B(1,0),C(-2,6).
(1)求经过点A,B,C三点的抛物线解析式.
(2)设直线BC交y轴于点E,连结AE,求证:AE=CE;
(3)设抛物线与y轴交于点D,连结AD交BC于点F,求证:以A,B,F为顶点的三角形与△ABC相似,并求: .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
永嘉县绿色和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我县收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为 元,试写出
元,试写出 与
与 之间的函数关系式.
之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数图象的顶点是(-1,2),且过点(0, ).
).
(1)求二次函数的表达式,并在图中画出它的图象;
(2)判断点(2, )是否在该二次函数图象上;并指出当
)是否在该二次函数图象上;并指出当 取何值时,
取何值时,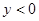 ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
抛物线 与y轴交于点(0,3).
与y轴交于点(0,3).
(1)求抛物线的解析式;(2分)
(2)求抛物线与坐标轴的交点坐标;(6分)
(3)① 当x取什么值时,y>0 ?
② 当x取什么值时,y的值随x的增大而减小?(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 的顶点为Q,与
的顶点为Q,与 轴交于A(-1,0)、B(5, 0)两点,与
轴交于A(-1,0)、B(5, 0)两点,与 轴交于C点.
轴交于C点.
(1)直接写出抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线的对称轴上求一点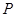 ,使得△
,使得△ 的周长最小.请在图中画出点
的周长最小.请在图中画出点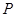 的位置,并求点
的位置,并求点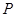 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,抛物线 的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com