
【题目】如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交线段PA、PB于C、D两点,若∠APB=40°,则∠COD的度数为( )
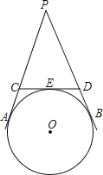
A.50°B.60°C.70°D.75°
科目:初中数学 来源: 题型:
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … |
| 0 |
| 1 |
| 2 |
| … |
y | … |
| ﹣1 |
| m |
| ﹣1 | n | … |
则对于该函数的性质的判断:①该二次函数有最大值;②不等式y>﹣1的解集是x<0或x>2;③方程ax2+bx+c=0的两个实数根分别位于﹣![]() <x<0和2<x<
<x<0和2<x<![]() 之间;④当x>0时,函数值y随x的增大而增大;其中正确的是( )
之间;④当x>0时,函数值y随x的增大而增大;其中正确的是( )
A.②③B.②④C.①③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,4),B(4,4),C(6,0).
(1)△ABC的面积是 .
(2)请以原点O为位似中心,画出△A'B'C',使它与△ABC的相似比为1:2,变换后点A、B的对应点分别为点A'、B',点B'在第一象限;
(3)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P' 的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
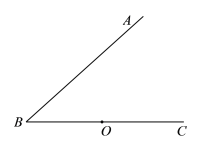
【题目】如图,点O为∠ABC的边![]() 上的一点,过点O作OM⊥AB于点
上的一点,过点O作OM⊥AB于点![]() ,到点
,到点![]() 的距离等于线段OM的长的所有点组成图形
的距离等于线段OM的长的所有点组成图形![]() .图形W与射线
.图形W与射线![]() 交于E,F两点(点在点F的左侧).
交于E,F两点(点在点F的左侧).
(1)过点![]() 作
作![]() 于点
于点![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的长;
,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠![]()
![]() ,判断射线BD与图形
,判断射线BD与图形![]() 公共点的个数,并证明.
公共点的个数,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像与x轴相交于点A,与y轴相交于点B,二次函数
的图像与x轴相交于点A,与y轴相交于点B,二次函数![]() 图像经过点A、B,与x轴相交于另一点C.
图像经过点A、B,与x轴相交于另一点C.
(1)求a、b的值;
(2)在直角坐标系中画出该二次函数的图像;
(3)求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
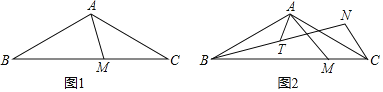
【题目】在△ABC中,AB=AC,∠BAC=120°,M为BC边上一动点(M不与B、C重合)
(1)如图1,若∠MAC=45°,求![]() ;
;
(2)如图2,将CM绕点C顺时针旋转60°至CN,连接BN,T为BN的中点,连接AT.
①求证:AM=2AT;
②当AB=AC=2时,直接写出CM+4AT的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
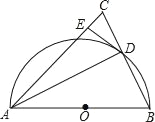
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)当⊙O半径为3,CE=2时,求BD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
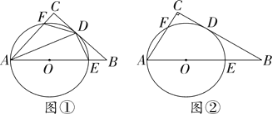
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() ,其顶点为A.
,其顶点为A.
(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
(2)直线BC平行于x轴,交这条抛物线于B、C两点(点B在点C左侧),且![]() ,求点B坐标.
,求点B坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com