
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA 为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点 ,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
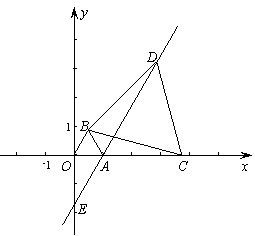
解:(1)∵△OAB和△BCD都为等边三角形,∴OB=AB,BC=BD,∠OBA=∠DBC=60°,即∠OBA+∠ABC=∠DBC+∠ABC,∴∠OBC=∠ABD,∴△OBC≌△ABD,∴AD=OC=1+x;
(2)随着C点的变化,直线AE的位置不变.理由如下:
由△OBC≌△ABD,得到∠BAD=∠BOC=60°,又∵∠BAO=60°,∴∠DAC=60°,
∴∠OAE=60°,又OA=1,
在直角三角形AOE中, OE=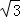 ,点E坐标为(0,﹣
,点E坐标为(0,﹣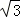 ),A(1,0),
),A(1,0),
设直线AE解析式为y=kx+b,把E和A的坐标代入得: ,
,
解得: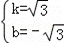 ,
,
所以直线AE的解析式为y=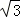 x﹣
x﹣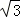 ;
;
(3)根据题意画出图形,如图所示:∵∠BOA=∠DAC=60°,EA∥OB,又EF∥OB,
则EF与EA所在的直线重合,∴点F为DE与BC的交点,又F为BC中点,∴A为OC中点,又AO=1,则OC=2,∴当C的坐标为(2,0)时,EF∥OB;这时直线BO与⊙F相切,理由如下:
∵△BCD为等边三角形,F为BC中点,∴DF⊥BC,又EF∥OB,∴FB⊥OB,即∠FBO=90°,
故直线BO与⊙F相切;
|
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
下列命题正确的有 ( )个
①400角为内角的两个等腰三角形必相似
②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为750
③一组对边平行,另一组对边相等的四边形是平行四边形
④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2∶b2∶c2=2∶1∶1
⑤若△ABC的三边a、 b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形。
b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形。
A、1个 B、2个 C、3个 D、4个
查看答案和解析>>
科目:初中数学 来源: 题型:
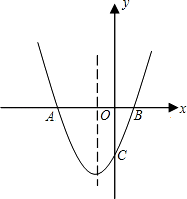
如图,抛物线y=(x+1)2+k与x轴交于A、B两点,与y轴交于点C(0,﹣3)
(1)求抛物线的对称轴及k的值;
(2)抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的一条弦,点C是⊙O上一动点, 且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF 与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为__________ .
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两个小组各10名同学进行英语口语会话练习,各练习5次,他们每个同学合格的次数分别如下:
甲组:4,1,2,2,1,3,3,1,2,1。
乙组:4,3,0,2,1,3,3,0,1,3。
(1).如果合格3次以上(含3次)作为及格标准,请你说明哪个小组 的及格率高?
的及格率高?
(2).试计算两个小组的方差,请你比较哪个小组的口语会话的合格次数比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
不能判定四边形ABCD是平行四边形的条件是( )
A.∠A=∠C  ∠B=∠D B.AB∥CD AD=BC C.AB∥CD ∠A=∠C D.AB∥CD AB=CD
∠B=∠D B.AB∥CD AD=BC C.AB∥CD ∠A=∠C D.AB∥CD AB=CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com