
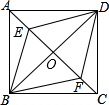
 如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是①③④(把所有正确结论的序号都填在横线上)
如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是①③④(把所有正确结论的序号都填在横线上)分析 根据正方形的性质、平行四边形的判定和性质以及菱形的判定方法逐项分析即可.
解答 解:
∵点E、F分别是AO、CO的中点,
∴OE=OF,
∵四边形ABCD是正方形,
∴OD=OB,AC⊥BD,
∴四边形BEDF是平行四边形,
∴BF=DE,故选项①正确;
∵四边形BEDF是平行四边形,AC⊥BD,
∴四边形BFDE是菱形,故选项④正确;
∵△AED的一边AE是△ACD的边AC的$\frac{1}{4}$,且此边的高相等,
∴S△ABD=$\frac{1}{4}$S△ACD;故选项③正确,
∵AB>BO,BE不垂直于AO,
∴BE不是∠ABO的角平分线,
∴∠ABO≠2∠ABE;故选项②没有足够的条件证明成立,
故答案为:①③④.
点评 本题考查了正方形的性质、平行四边形的判定和性质以及菱形的判定方法,题目的综合性较强,难度不大,熟记各种特殊的四边形的判定方法和性质是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 80 | B. | 110 | C. | 140 | D. | 220 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
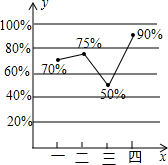 某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 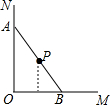 | B. | 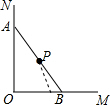 | C. | 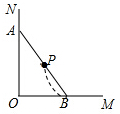 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
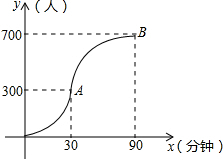 科技馆是少年儿童节假日游玩的乐园.
科技馆是少年儿童节假日游玩的乐园.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
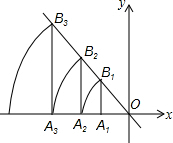 如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).
如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-x+y)(x-y) | B. | (y-1)(-1-y) | C. | (x-2)(y+2) | D. | (2x+y)(2y-x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com