
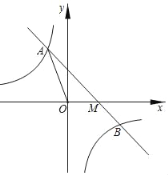
【题目】如图,已知一次函数y=﹣x+2与反比例函数y=![]() 与的图象交于A,B两点,与x轴交于点M,且点A的横坐标是﹣2,B点的横坐标是4.
与的图象交于A,B两点,与x轴交于点M,且点A的横坐标是﹣2,B点的横坐标是4.
(1)求反比例函数的解析式;
(2)求△AOM的面积;
(3)根据图象直接写出反比例函数值大于一次函数值时x的取值范围.
【答案】(1)为y=﹣![]() ;(2)4;(3)﹣2<x<0或x>4.
;(2)4;(3)﹣2<x<0或x>4.
【解析】
(1)依据点A的横坐标是﹣2,B点的横坐标是4,即可得到A(﹣2,4),B(4,﹣2),再根据待定系数法求出反比例函数的解析式;
(2)求出直线AB与x轴的交点M的坐标,根据三角形的面积公式求出△AOM的面积即可;
(3)利用函数图象求出使反比例函数值大于一次函数值时自变量x的取值范围.
(1)∵点A的横坐标是﹣2,B点的横坐标是4,
∴当x=﹣2时,y=﹣(﹣2)+2=4,
当x=4时,y=﹣4+2=﹣2,
∴A(﹣2,4),B(4,﹣2),
∵反比例函数y=![]() 的图象经过A,B两点,
的图象经过A,B两点,
∴k=﹣2×4=﹣8,
∴反比例函数的解析式为y=﹣![]() ;
;
(2)一次函数y=﹣x+2中,令y=0,则x=2,
∴M(2,0),即MO=2,
∴△AOM的面积=![]() ×OM×|yA|=
×OM×|yA|=![]() ×2×4=4;
×2×4=4;
(3)∵A(﹣2,4),B(4,﹣2),
∴由图象可得,反比例函数值大于一次函数值时x的取值范围为:﹣2<x<0或x>4.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2﹣2x+3.
(1)把函数关系式配成顶点式并求出图象的顶点坐标和对称轴.
(2)若图象与x轴交点为A.B,与y轴交点为C,求A、B、C三点的坐标;
(3)在图中画出图象.并求出△ABC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ;
;![]() 按此做法进行下去,其中
按此做法进行下去,其中![]() 的长为______.
的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,AC=BC=2,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )

A. π B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
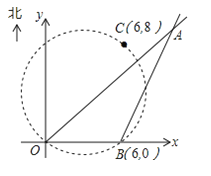
【题目】在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
(1)某时刻海面上出现一渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离.(![]() )
)
(2)若渔船A由(1)中位置向正西方向航行,是否会进入海洋生物保护区?通过计算回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
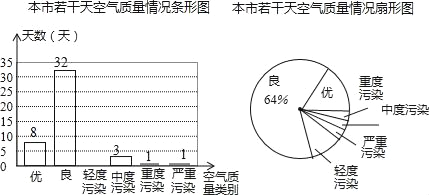
【题目】为了解哈市今年的空气质量情况,环保部门从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图不完整的统计图:
(1)计算被抽取的天数;
(2)请通过计算补全条形统计图;
(3)请估计哈市这一年(365天)达到优和良的总天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
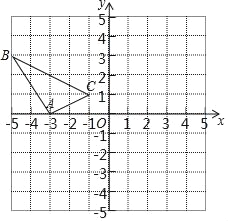
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com