
【题目】如图,△ABC是边长为1的等边三角形,过点C的直线m平行AB,D、E分别是线段AB、直线m上的点,先按如图方式进行折叠,点A、C分别落在A′、C′处,且A′C′经过点B,DE为折痕,当C′E⊥m时,![]() 的值为_____.
的值为_____.
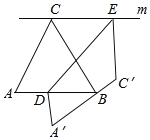
【答案】1+![]()
【解析】
由折叠的性质得出∠C′ED=∠CED=45°,由平行线的性质得出∠BDE=∠DEC=45°,再由等边三角形的性质得出AB=AC=1,∠A=∠ABC=∠ACB=60°,求出∠DFB=∠CFE=75°,得出∠BCE=60°,∠ACE=∠C′=120°,证出∠A′DB=90°,由直角三角形的性质得出A′B=2A′D,设AD=x,则BA′=2x,BD=1-x,A′D=x,BC′=1-2x,在Rt△A′BD中,由勾股定理得出方程,解方程求出x的值,即可得出结果.
∵C′E⊥m,
∴∠CEC′=90°,
∵DE为折痕,
∴∠C′ED=∠CED=45°,
∵m∥AB,
∴∠BDE=∠DEC=45°,
∵△ABC是等边三角形,
∴AB=AC=1,∠A=∠ABC=∠ACB=60°,
设CB与DE交于点F,如图所示:
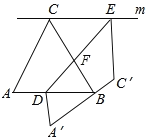
则∠DFB=∠CFE=75°,
∴∠BCE=60°,
∴∠ACE=∠C′=120°,
∵∠A=∠A′=60°,
∴∠A′DE=135°,
∴∠A′DB=90°,
∴A′B=2A′D,
∵A′D=AD,
设AD=x,则BA′=2x,BD=1﹣x,A′D=x,BC′=1﹣2x,
在Rt△A′BD中,由勾股定理得:x2+(1﹣x)2=(2x)2,
解得:x=![]() (负值舍去),
(负值舍去),
∴x=![]() ,
,
∴BA'=﹣1+![]() ,BC'=1﹣(﹣1+
,BC'=1﹣(﹣1+![]() )=2﹣
)=2﹣![]() ,
,
∴![]() =
=![]() =1+
=1+![]() ;
;
故答案为:1+![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
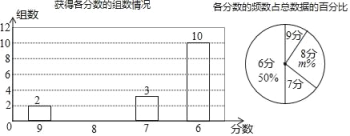
【题目】目前由重庆市教育委员会,渝北区人们政府主办的“阳光下成长”重庆市第八届中小学生艺术展演活动落下帷幕,重庆一中学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖,重庆一中获优秀组织奖,重庆一中老师李珊获先进个人奖,其中重庆一中舞蹈团将代表重庆市参加明年的全国集中展演比赛,若以下两个统计图统计了舞蹈组各代表队的得分情况:
(1)m= ,在扇形统计图中分数为7的圆心角度数为 度.
(2)补全条形统计图,各组得分的中位数是 分,众数是 分.
(3)若舞蹈组获得一等奖的队伍有2组,已知主办方各组的奖项个数是按相同比例设置的,若参加该展演活动的总队伍数共有120组,那么该展演活动共产生了多少个一等奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?为什么?
(3)探究:腰长为![]() 的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
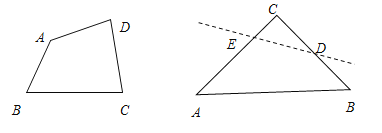
查看答案和解析>>
科目:初中数学 来源: 题型:
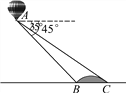
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com