
【题目】若关于x,y的二元一次方程组![]() 的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求m的值.
的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求m的值.
【答案】![]()
【解析】
首先用含m的式子表示x和y,由于x、y的值是一个等腰三角形两边的长,所以x、y可能是腰也可能是底,依次分析即可解决,注意应根据三角形三边关系验证是否能组成三角形.
解: ,
,
②×2①得:x=m1,
①×2②得:y=2,
①当x、y都是腰时,m1=2,
解得m=3,
则底为:922=5,
∵2+2<5,
∴不能组成三角形;
②当y=2为底,x为腰,2x+2=9
x=3.5,三边为:3.5,3.5,2,可以组成三角形,
x=m1=3.5,
解得m=4.5;
③x=m1是底,y=2是腰
2y+x=9,解得x=5,
三边为:5,2,2,不能构成三角形,
x=m1=5
解得m=6不符合题意,
综上所述:m的值为4.5.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= ![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= ![]() BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A′B′C′是△ABC 经过平移得到的,△ABC 中任意一点 P(x1,y1)平移后的对应点为 P′(x1+6,y1﹣5).
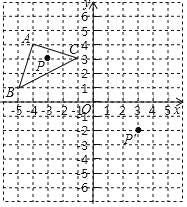
(1)请写出三角形 ABC 平移的过程;
(2)分别写出点 A′,B′,C′的坐标;
(3)画出平移后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点F是对角线BD上的一点,EF∥AB交AD于点E,FG∥BC交DC于点G,四边形EFGP是平行四边形,给出如下结论:
①四边形EFGP是菱形;
②△PED为等腰三角形;
③若∠ABD=90°,则△EFP≌△GPD;
④若四边形FPDG也是平行四边形,则BC∥AD且∠CDA=60°.
其中正确的结论的序号是(把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(数学实验)如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干个可以拼出一些长方形来解释某些等式.例如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.

(初步运用)
(1)仿照例子,图③可以解释为: ;
(2)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+3b)、(a+5b),不画图形,试通过计算说明需要C类卡片多少张;
(拓展运用)
若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积为2a2+5ab+3b2,通过操作你会发现拼成的长方形的长宽分别是 ,将2a2+5ab+3b2改写成几个整式积的形式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某航空公司托运行李的费用y(元)与行李的质量x(千克)之间的关系,由图可以看出:
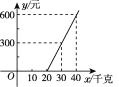
(1)当行李质量为30千克时,行李托运费是________元;
(2)当行李质量为________千克时,行李托运费是600元;
(3)每位旅客最多可以免费携带________千克的行李.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com