
【题目】如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论:
①△BDF,△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长为AB+AC;
④BD=CE.其中正确的是 .

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形(长方形),点A、C的坐标分别为A(10,0 ),C(0,4),点D是OA的中点,点P在线段BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 ____________________________________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
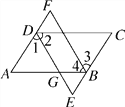
【题目】(南阳唐河县期中)如图,在ABCD中,DE平分∠ADC交AB于G,交CB的延长线于E,BF平分∠ABC交AD的延长线于F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y=![]() x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC. 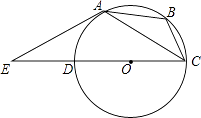
(1)求∠B的度数;
(2)若ED=1,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
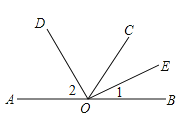
【题目】如图,O是直线AB上的一点,C是直线AB外的一点,OD是∠AOC的平分线,
OE是∠COB的平分线.
(1)已知∠1=23°,求∠2的度数;
(2)无论点C的位置如何改变,图中是否存在一个角,它的大小始终不变(∠AOB除外)?如果存在,求出这个角的度数;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com