
【题目】如图,点F是CD 的中点,且AF⊥CD,BC=ED,∠BCD=∠EDC.
(1)求证:BF=EF;
(2)求证:AB=AE.

【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据中点定义可得CF=DF,然后证明△BCF≌△EDF,进而可得FB=FE;(2)、根据△BCF≌△EDF可得FB=EF,∠BFC=∠EFD,再证明∠BFA=∠EFA,然后判定△ABF≌△AEF可得AB=AE.
试题解析:(1)、∵点F是CD 的中点, ∴CF=DF,
在△BCF和△EDF中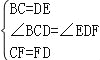 , ∴△BCF≌△EDF(SAS), ∴FB=FE;
, ∴△BCF≌△EDF(SAS), ∴FB=FE;
(2)、∵△BCF≌△EDF, ∴FB=EF,∠BFC=∠EFD, ∵AF⊥CD, ∴∠BFC+∠AFB=∠AFE+∠EFD,
∴∠BFA=∠EFA, 在△ABF和△AEF中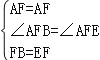 , ∴△ABF≌△AEF(SAS), ∴AB=AE.
, ∴△ABF≌△AEF(SAS), ∴AB=AE.


科目:初中数学 来源: 题型:
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 在所有连接两点的线中,直线最短 B. 射线OA与射线AO表示的是同一条射线
C. 连接两点的线段,叫做两点间的距离 D. 两点确定一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒 ![]() 个单位长度,则第2017秒时,点P的坐标是( )
个单位长度,则第2017秒时,点P的坐标是( )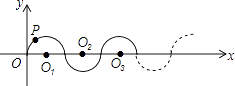
A.(2016,0)
B.(2017,1)
C.(2017,﹣1)
D.(2018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算结果正确的是( )
A.﹣2x2y3x3y3=﹣2x6y9B.12x6y4÷2x3y3=6x3y
C.3x3y2﹣x2y3=xyD.(﹣2a﹣3)(2a﹣3)=4a2﹣9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com