
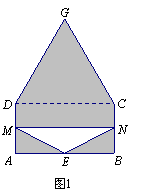
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积;
(2)设MN与AB之间的距离为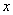 米,试将△EMN的面积S(平方米)表示成关于x的函数;
米,试将△EMN的面积S(平方米)表示成关于x的函数;
(3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.
解:(1)由题意,当MN和AB之间的距离为0.5米时,MN应位于DC下方,且此时△EMN中MN边上的高为0.5米.
 所以,S△EMN=
所以,S△EMN= =0.5(平方米).
=0.5(平方米).
即△EMN的面积为0.5平方米.
(2)①如图1所示,当MN在矩形区域滑动,
即0<x≤1时,
△EMN的面积S=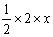 =
=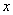 ;
;
②如图2所示,当MN在三角形区域滑动,
即1<x<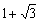 时,
时,
如图,连接EG,交CD于点F,交MN于点H,
∵ E为AB中点,
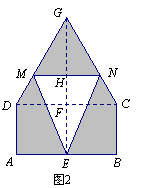 ∴ F为CD中点,GF⊥CD,且FG=
∴ F为CD中点,GF⊥CD,且FG=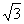 .
.
又∵ MN∥CD,
∴ △MNG∽△DCG.
∴ 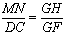 ,即
,即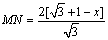
故△EMN的面积S=
=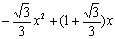 ;
;
综合可得:
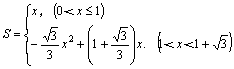
(3)①当MN在矩形区域滑动时,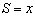 ,所以有
,所以有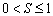 ;
;
②当MN在三角形区域滑动时,S=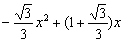 .
.
因而,当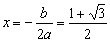 (米)时,S得到最大值,
(米)时,S得到最大值,
最大值S=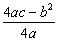 =
=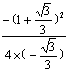 =
=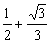 (平方米).
(平方米).
∵ 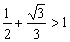
∴ S有最大值,最大值为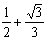 平方米.
平方米.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
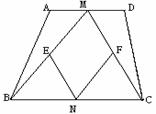
如图,在等腰梯形ABCD中,M、N分别为AD、BC的中点,E、F分别为BM、CM的中点。
(1)求证:△ABM≌△CDM;
(2)判断并证明四边形MENF是何种特殊的四边形;
‚当等腰梯形ABCD的高h与底边BC满足怎样的数量关系时,四边形MENF是正方形?(直接写出结论,不需要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
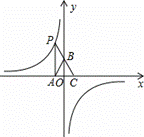 如图,点P是反比例函数
如图,点P是反比例函数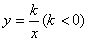 图象上的点,PA垂直
图象上的点,PA垂直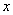 轴于点A(-1,0),点C的坐标为(1,0),PC交
轴于点A(-1,0),点C的坐标为(1,0),PC交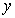 轴于点B,连结AB,已知AB=
轴于点B,连结AB,已知AB=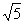
(1)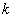 的值是__________;
的值是__________;
(2)若M( ,
, )是该反比例函数图象上的点,且满足
)是该反比例函数图象上的点,且满足
∠MBA<∠ABC,则 的取值范围是__________
的取值范围是__________
查看答案和解析>>
科目:初中数学 来源: 题型:
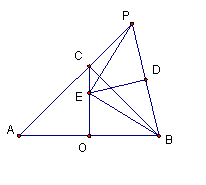
如图,AB为等腰直角⊿ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论,其中正确的个数是( )
①E为⊿ABP的外心; ②∠PEB=90°;
③PC·BE = OE·PB; ④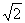 CE + PC=
CE + PC=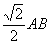 .
.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
有下面3个结论: ① 存在两个不同的无理数, 它们的积是整数; ② 存在两个不同的无理数, 它们的差是整数; ③ 存在两个不同的非整数的有理数, 它们的和与商都是整数. 先判断这3个结论分别是正确还是错误的, 如果正确, 请举出符合结论的两个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
设边长为4的正方形的对角线长为a,下列关于a的四种说法: a是无理数;‚ a可以用数轴上的一个点来表示;ƒ 4<a<5; „ a是32的算术平方根。其中,所有正确说法的序号是 ( )
A. „ B. ‚ƒ C. ‚„ D. ƒ„
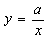 | |||
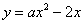 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线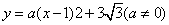 经过点
经过点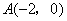 ,抛物线的顶点为
,抛物线的顶点为 ,过
,过 作射线
作射线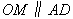 .过顶点
.过顶点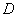 平行于
平行于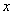 轴的直线交射线
轴的直线交射线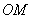 于点
于点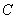 ,
,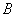 在
在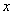 轴正半轴上,连结
轴正半轴上,连结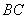 .
.
(1)求该抛物线的解析式;
(2)若动点 从点
从点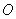 出发,以每秒1个长度单位的速度沿射线
出发,以每秒1个长度单位的速度沿射线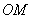 运动,设点
运动,设点 运动的时间为
运动的时间为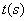 .问当
.问当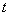 为何值时,四边形
为何值时,四边形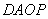 分别为平行四边形?直角梯形?等腰梯形?
分别为平行四边形?直角梯形?等腰梯形?
(3)若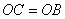 ,动点
,动点 和动点
和动点 分别从点
分别从点 和点
和点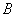 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿
同时出发,分别以每秒1个长度单位和2个长度单位的速度沿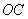 和
和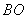 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为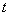
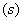 ,连接
,连接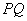 ,当
,当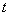 为何值时,四边形
为何值时,四边形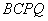 的面积最小?并求出最小值及此时
的面积最小?并求出最小值及此时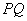 的长.
的长.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com