已知抛物线y=ax2+bx+c(a>0)的顶点是C(0,1),直线l:y=-ax+3与这条抛物线交于P、Q两点,与x轴、y轴分别交于点M和N.
(1)设点P到x轴的距离为2,试求直线l的函数关系式;
(2)若线段MP与PN的长度之比为3:1,试求抛物线的函数关系式.
分析:(1)由于抛物线的顶点为C(0,1),因此抛物线的解析式中b=0,c=1.即抛物线的解析式为y=ax2+1.已知了P到x轴的距离为2,即P点的纵坐标为2.可根据直线l的解析式求出P点的坐标,然后将P点坐标代入抛物线的解析式中即可求得a的值,也就能求出直线l的函数关系式.
(2)本题要根据相似三角形来求.已知了线段MP与PN的长度之比为3:1,如果过P作x轴的垂线,根据平行线分线段成比例定理即可得出P点的纵坐标的值.进而可仿照(1)的方法,先代入直线的解析式,然后再代入抛物线中即可求出a的值,也就求出了抛物线的解析式.
解答:解:(1)∵抛物线的顶点是C(0,1),
∴b=0,c=1,
∴y=ax
2+1.
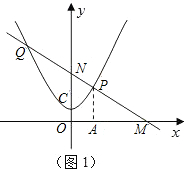
如图1,∵a>0,直线l过点N(0,3),
∴M点在x轴正半轴上.
∵点P到x轴的距离为2,
即点P的纵坐标为2.
把y=2代入y=-ax+3
得,x=
,
∴P点坐标为(
,2).
∵直线与抛物线交于点P,
∴点P在y=ax
2+1上,
∴2=a•(
)
2+1,
∴a=1.
∴直线l的函数关系式为y=-x+3.
(2)如图1,若点P在y轴的右边,记为P
1过点P
1作P
1A⊥x轴于A,
∵∠P
1MA=∠NMO,
∴Rt△MP
1A∽Rt△MNO,
∴
=.
∵
=,
∴MP
1=3P
1N,MN=MP
1+P
1N=4P
1N
∴
=,
即
=,
∵ON=3,
∴P
1A=
,
即点P
1的纵坐标为
.
把y=
代入y=-ax+3,
得x=
,
∴点P
1的坐标为(
,
).
又∵点P
1是直线l与抛物线的交点,
∴点P
1在抛物线y=ax
2+1上,
∴
=a•(
)
2+1,
∴a=
.
抛物线的函数关系式为y=
x
2+1.
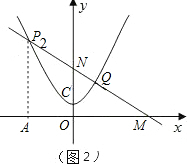
如图2,若点P在y轴的左边,记为P
2.作P
2A⊥x轴于A,
∵∠P
2MA=∠NMO,
∴Rt△MP
2A∽Rt△MNO,
∴
=
.
∵
=,
∴MP
2=3P
2N,MN=MP
2-P
2N=2P
2N,
∴
=,即
=
,
∵ON=3,
∴P
2A=
,即即点P
2的纵坐标为
.
由P
2在直线l上可求得P
2(-
,
),
又∵P
2在抛物线上,
∴
=a•(-
)
2+1,
∴a=
.
∴抛物线的函数关系式为y=
x
2+1.
点评:本题主要考查了一次函数与二次函数解析式的确定以及函数图象交点等知识.





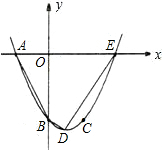 与x轴的另一个交点为E.
与x轴的另一个交点为E.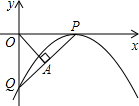 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=