
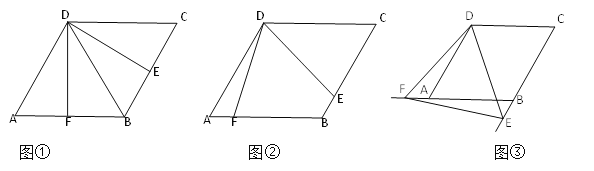
【题目】如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,![]() EDF=60°,当CE=AF时,如图①小芳同学得出的结论是DE=DF。
EDF=60°,当CE=AF时,如图①小芳同学得出的结论是DE=DF。
(1)继续旋转三角形纸片,当CE![]() AF时,如图②,小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由。
AF时,如图②,小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由。
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图③,请写出DE与DF的数量关系,并加以证明。
(3)连接EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
【答案】(1)DF=DE.理由见解析;(2)DF=DE.理由见解析;(3)![]() ,当x=1时,
,当x=1时, ![]()
【解析】(1)DF=DE.理由如下:
如答图1,连接BD.

∵四边形ABCD是菱形,
∴AD=AB.
又∵∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠DAF=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
∵在△ADF与△BDE中,
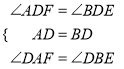 ,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(2)DF=DE.理由如下:
如答图2,连接BD.
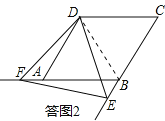
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠DAF=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
∵在△ADF与△BDE中,
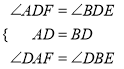 ,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
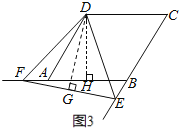
(3)由(2)知,DE=DF,又∵∠EDF=60°,
∴△DEF是等边三角形,
∵四边形ABCD是边长为2的菱形,
∴DH=![]() ,
,
∵BF=CE=x,
∴AF=x-2,
∴FH=AF+AH=x-2+1=x-1,
∴DF=![]() ,DG=
,DG=![]() ×
×![]() ,
,
∴y=S△DEF=![]() ×EF×DG=
×EF×DG=![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() (x-1)2+
(x-1)2+![]() .
.
∴当x=1时,y最小值=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了__s时,以C点为圆心,1.5cm为半径的圆与直线EF相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由四个小正方形拼接成的L形图案,按下列 要求画出图形。

(1)请你用两种方法分别在L形图案中添画一个小正方形,使它成为轴对称图形;
(2)请你在L形图案中添画一个小正方形,使它成为中心对称图形。
(3)请你在L}形图案中移动一个小正方形,使它成为既是中心对称图形,又是轴对称图形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论正确的有________________.
①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.
秒时,△PBQ为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m-1)x2-x-2=0,
(1)若x=-1是方程的一个根,求m的值及另一个根;
(2)当m为何值时方程有两个不同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 . (填写所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com